6. Controle e Monitoramento de Produto ou Processo 6.4. Introdução à Analise de Séries Temporais 6.4.4. Modelos Univariados de Séries Temporais 6.4.4.5. Modelos Box-Jenkins/H2>
Abordagem de Box-Jenkins	O modelo ARMA de Box-Jenkins é uma combinação dos modelos AR e MA (descritos na página anterior): onde os termos na equação tem o mesmo significado dado para os modelos AR e MA.
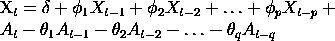
Comentários sobre o Modelo de Box-Jenkins	Um par de notas sobre este modelo. O modelo de Box-Jenkins assume que a série temporal é estacionária. Box e Jenkins recomendaram a diferenciação de séries não estacionárias em uma ou mais vezes até atingir a estacionariedade. Fazendo isto se produz um modelo ARIMA, com o "I" significando "Integrado". Algumas formulações transformam a série subtraindo a média da série de cada ponto de dado. Isto leva a uma série com média zero. Se você precisar fazer isto ou não é dependente de software você usa para estimar o modelo. Os modelos de Box-Jenkins podem ser estendidos para incluirem sazonalidade nos termos autoregressivos e média móveis sazonais. Embora isto complica a notação e a matemática do modelo, os conceitos subjacentes para os termos de média móvel sazonal e autoregressivo sazonal são similares aos termos de média móvel e autoregressivos não sazonais. O modelo mais geral de Box-Jenkins inclui operadores de diferenciação, termos autoregressivos, termos de média móvel, operadores de diferenciação sazonais, termos autoregressivos sazonais, e termos de médias móveis sazonais. Como com as modelagens em geral, entretanto, somente termos necessários deverão ser incluídos no modelo. Aquels interessados nos detalhes matemáticos podem consultar Box, Jenkins e Reisel (1994), Chatfield (1996), or Brockwell e Davis (2002).
Estágios na Modelagem de Box-Jenkins	Existem três estágios principais na construção de um modelo de ´serie temporal de Box-Jenkins. Identificação do Modelo Estimação do Modelo Validação do Modelo
Observações	A observação seguinte a respeito dos modelos de Box-Jenkins deverá ser notada. Os modelos de Box-Jenkins são muito flexíveis devido à inclusão dos termos de média móvel e autoregressivos. Baseado no teorema de decomposição de Wold (não discutido aqui), um processo estacionário pode ser aproximado pelo modelo ARMA. Na prática, encontrar esta aproximação pode não ser fácil. Chatfield (1996) recomenda métodos de decomposição para séries em que os componentes de tendência e sazonalidade são dominantes. Construir bons modelos ARIMA geralmente exige mais experiência do que os métodos estatísitcos usados tal como regressão.
Exigência de Séries Suficientemente Longas	Geralmente, o ajuste efetivo dos modelos de Box-Jenkins exige no mínimo séries moderadamente longas. Chatfield (1996) recomendam no mínimo 50 observações. Muitos outros recomendariam no mínimo 100 observações.