6.4. Introdução à Analise de Séries Temporais
6.4.4. Modelos Univariados de Séries Temporais
6.4.4.3. |
Sazonalidade |
Sazonalidade é muito comum nas séries temporais econômicas. Ela é menos comum nos dados científicos e de engenharia.
Se a sazonalidade estiver presente, ela deve ser incorporada no modelo de série temporal. Nesta seção, discutimos técnicas para detectar sazonalidade. Adiaremos a modelagem da sazonalidade até as últimas seções.
- A gráfico run sequence frequentemente mostrará sazonalidade.
- A gráfico de subséries sazonais é uma técnica especializada para mostrar sazonalidade.
- Múltiplos box gráficos podem ser usados como uma alternativa para o gráfico de subséries sazonais para detectar a sazonalidade.
- O gráfico autocorrelação pode ajudar a identificar sazonalidade.
O gráfico sequence plot é recomendado como primeiro passo para analisar qualquer série temporal. Embora a sazonalidade possa algumas vezes ser indicada com este gráfico, a sazonalidade é mostrada mais claramente pelo gráfico da subsérie sazonal ou gráfico box. O gráfico das subséries sazonais faz um excelente trabalho de mostrar as diferenças sazonais (entre padrões agrupados) e também nos padrões interiores aos grupos. O gráfico box mostra a diferença sazonal (padrões entre grupos) muito bem, mas não mostra padrões internos do grupo. Entretanto, para conjunto de dados grandes, o gráfico box é usualmente mais fácil para ler do que o gráfico de subséries sazonais.
O gráfico de subséries sazonais e o gráfico box assumem que os períodos sazonais sejam conhecidos. Na maioria dos casos, o analista de fato conhecerá isto. Por exemplo, para dados mensais, o período é 12 já que existem 12 meses num ano. Entretanto, se o período não for conhecido, o gráfico de autocorrelação pode ajudar. Se existir sazonalidade significativa, o gráfico de autocorrelação deverá mostrar estacas nos lags iguais ao período. Por exemplo, para dados mensais, se existir um efeito de sazonalidade, poderemos esperar ver picos nos lag 12, 24, 36, e assim por diante (embora a intensidade possa decrescer quanto mais longe estivermos).
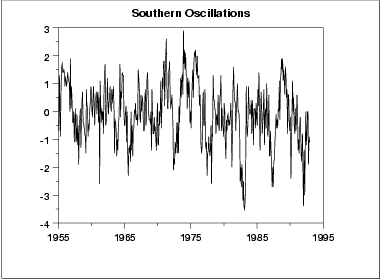
Padrões periódicos não óbvios são aparentes no gráfico run sequence.
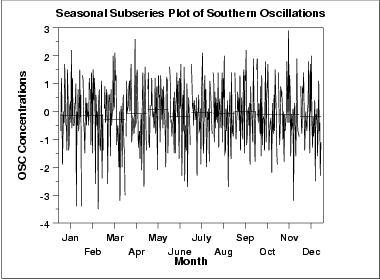
As médias de cada mês são relativamente próximas e mostram padrões não óbvios.
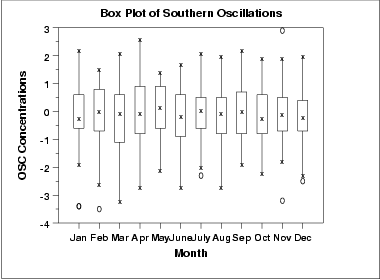
Como com o gráfico de subséries sazonais, padrões sazonais não óbvios são aparentes.
Devido ao número muito grande de observações, o gráfico box mostra a diferença entre meses melhor do que o gráfico de subséries sazonais.
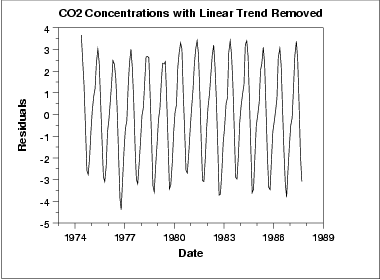
Este gráfico mostra comportamento periódico. Entretanto, é difícil determinar a natureza da sazonalidade deste gráfico.
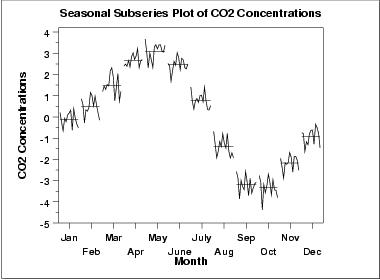
O gráfico de subséries sazonais mostram o padrão sazonal mais claramente. Neste caso, as concentrações de CO2 são mínimas em Setembro e Outubro. Daí, as concentrações crescem constantemente até Junho e começam a decrescer até Setembro.
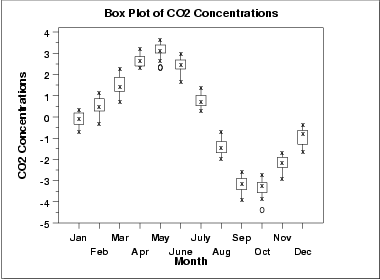
Como com o gráfico da subsérie sazonal, o padrão sazonal é bem evidente no box plot.

