6.4. Introdução à Analise de Séries Temporais
6.4.4. Modelos Univariados de Séries Temporais
6.4.4.2. |
Estacionariedade |
Um processo estacionário tem a propriedade de que a média, variância e estrutura de autocorrelação não mudam no decorrer do tempo. Estacionariedade pode ser definida em termos matemáticos precisos, mas para os nossos propósitos queremos dizer uma série parecida com um plano liso, sem tendência, variância constante no decorrer do tempo, um estrutura de autocorrelação constante no decorrer do tempo e nenhuma flutuação periódica (sazonalidadae).
Para propósitos práticos, estacionariedade pode geralmente ser determinada de um gráfico sequencial.
- Podemos diferenciar os dados. Isto é, dada a série
Zt, criamos a nova série
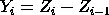
Os dados diferenciados conterão um ponto a menos que os dados originais. Embora você possa diferenciar os dados mais que uma vez, uma diferenciação é geralmente suficiente.
- Se os dados tiverem uma tendência, podemos ajustar algum tipo de curva aos dados e depois então modelar os resíduos daquele ajuste. Desde que o propósito do ajuste é simplesmente remover tendências de longo prazo, um ajuste simples, tal como uma linha reta, é tipicamente usado.
- Parta variância não constante, tomando o logarítmo ou a raiz quadrada da série pode estabilizar a variância. Para dados negativos, você pode adicionar uma constante adequada para tornar todos os dados positivos antes de aplicar a transformação. Esta constante pode então ser subtraída do modelo para obter valores previstos (i.e., ajustados) e previsões para pontos futuros.
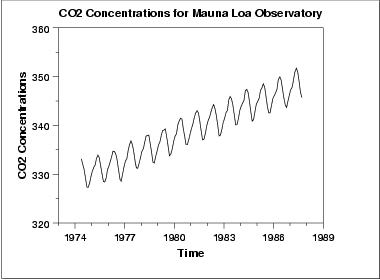
O gráfico sequancial inicial dos dados indica uma tendência crescente. Uma inspeção visual deste gráfico indica que um simples ajuste linear deverá ser suficiente para remover esta tendência para cima.
Este gráfico mostra também o comportamento periódico. Isto é discutido na próxima seção.
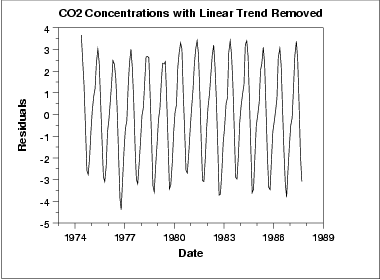
Este gráfico contém os resíduos de um ajuste linear aos dados originais. Após remover a tendência linear, o gráfico sequencial indica que os dados têm uma localização e variância constantes, embora o padrão dos resíduos mostre que os dados desviam do modelo de manira sistemática.

