Vivemos num espaço com três diferentes graus de liberdade para o movimento. Podemos ir para a esquerda ou para a direita. Podemos ir para frente ou para trás. Podemos ir para cima ou para baixo. Não são permitadas outras opções. Qualquer movimento que fazemos deve ser alguma combinação destes graus de liberdade.Qualquer ponto no nosso espaço pode ser atingido por combinação destes três tipos possíveis de movimento. Movimentos para cima ou para baixo são difícieis para os humanos. Estamos atados à superfície da Terra pela gravidade. Então não é difícil para nós andarmos para qualquer lugar ao longo da superfície não obstruída por objetos, mas achamos difícil voar para cima e daí para baixo. O espaço é mais 3-D para um pássaro ou um peixe do que é para nós.
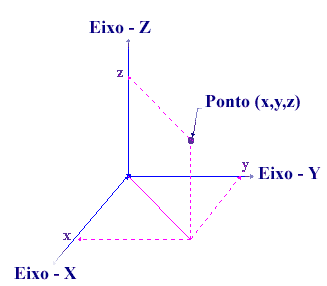
| Duas dimensões requerem somente dois números para especificar a localização de qualquer ponto. Existem dois graus de liberdade em 2-D. | Três dimensões requerem três números para especificar a localização de qualquer ponto. Existem três graus de liberdade em 3-D. |
 |
 |
![]()
Uma breve história das idéias sobre dimensionalidade.
Euclides: Na formulação da geometria de euclidiana uma quarta dimensão não foi certamente considerada.
Aristóteles: Foi a primeira pessoa a estabelecer categoricamente que a quarta dimensão é impossível. No seu trabalho 'Sobre o Céu' ele escreveu, "A linha tem magnitude em um modo, o plano em dois modos, e o sólido em três modos, e além destes não existe outra magnitude porque as três são todas elas."
Ptolomeu:(150,d.C) No seu livro 'Sobre a Distância' Ptolomeu deu uma 'prova' que a quarta dimensão é impossível. Ele sugeriu que se desenhassem três linhas mutuamente perpendiculares. Tente desenhar uma outra linha perpendicular a todas estas linhas. É impossível. A quarta linha perpendicular é "inteiramente sem medida e sem definição". A quarta dimensão é impossível. Esta não é realmente uma prov legítima da 4ª dimensão. Ela é meramente uma prova de que não podemos visualizar a 4ª dimensão.
Riemann: Em 10 de Junho de 1854 um novo modo de observar a geometria foi apresentado numa famosa aula pelo matemático Bernhard Riemann. Ele generalizou a geometria euclidiana para uma geometria não-euclidiana concedendo superfícies curvadas e qualquer número de dimensões superiores.
As idéias de Riemann fizeram muitas pessoas começarem a pensar sobre as dimensões mais altas. As pessoas encontraram que as ramificações da existência da dimensões mais elevadas eram assustadoras. Se você puder manipular a quarta dimensão ou dimensões superiores, você terá os poderes semelhantes aos de Deus.
Você poderá andar de tal modo que nenhuma parede poderá detê-lo.
Você aparecerá aos outros atravessando paredes e portas.
Quando estiver com fome, você poderá simplesmente entrar no refrigerador, sem abrir a porta.
Você poderá extrair uma seção de uma laranja sem descascá-la.
Você poderá fazer cirurgias sem cortar a pele.
Você poderá desaparecer e reaparecer à vontade.
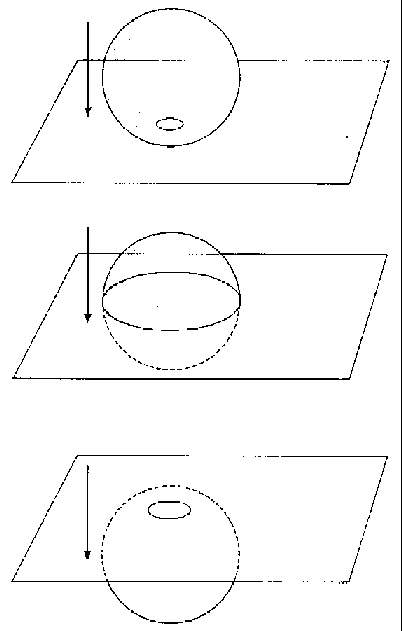
Você será capaz de ver as pessoas que foram enterradas por uma avalanche. O método padrão pelo qual as pessoas tentam entender as dimensões superiores é tentar ver como uma criatura de mais baixa dimensão veria um mundo tridimensional. Para este propósito o mundo 2-D é freqüentemente usado. Vamos considerar um mundo 2-D. Para aprisionar um criminoso num tal mundo, tería de ser colocado em volta dele uma delimitação circular. Para libertá-lo, tudo que uma criatura 3-D tem de fazer é desgarrá-lo do mundo 2-D, e depositá-lo novamente em outra parte de seu mundo. Esta façanha, que é muito comum no 3-D, parece fantástica no 2-D. Ninguém no mundo 2-D entende o que significa a direção para cima. Os órgãos internos de uma criatura 2-D seriam visíveis para nós. Seria trivial penetrar numa criatura 2-D e fazer cirurgia sem cortar a pele. Observando este mundo plano, notamos que somos onipotentes. A criatura 2-D não pode se ocultar de nós. Ela nos veria como tendo poderes mágicos.
No final dos anos de 1800, a idéia de uma quarta dimensão tornou-se muito popular. Em 1877, uma acusação escandalosa em Londres deu à idéia de dimensões extra uma notoriedade internacional. Um mágico e paranormal de nome Henry Slade foi preso por usar fraudulentamente quiromancia e etc., para enganar seus clientes. Físicos proeminentes da época vieram em defesa de Slade reivindicando que seus feitos paranormais realmente provaram que ele poderia invocar espíritos da quarta dimensão. Os detratores disseram que os cientistas, por estarem treinados a confiarem em seus sentidos, são as piores pessoas possíveis para avaliarem um mágico. Para objetivamente testar um mágico/paranormal precisar-se-ia de um outro mágico. Eles saberiam quando algum truque estivesse sendo feito.
Flatland
Em 1884 um diretor de escola em Londres, chamado Edwin Abbott (1838-1926) publicou uma novela satírica chamada 'Flatland: Um Romance de Muitas dimensões.' Este livro trabalha em vários níveis esboçados abaixo.
Flatland é uma estória que pode ser interpretada de vários modos.
(1) É uma sátira sobre a estagnada e insensível sociedade Victoriana, um lugar cheio de fanatismo e preconceitos sufocantes. "Incapazes" (aleijados) são postos a morrerem, mulheres não tem os seus direitos por completo, e quando o protagonista da estória Sr. A. Square tenta ensinar a seus discípulos sobre a terceira dimensão, ele é aprisionado.
(2) É um trabalho científico. Pensando sobre as dificuldades de A. Square no entendimento da terceira dimensão, tornamo-nos bem mais capazes de tratar com nossos próprios problemas da quarta dimensão.
(3) Num nível mais profundo, podemos talvez ver Flatland como um caminho indireto de Abbott falar sobre algumas experiências espirituais intensas.
----------------------------------------------
Flatland é um plano habitado por criaturas que escorregam sobre ele. As classes mais baixas no Flatland são triângulos com somente dois lados iguais.
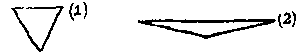
As classes superiores são objetos com todos os lados iguais. Quanto mais lados se tem em Flatland, maior será o seu status social. A maior classe social de todas é aquela dos objetos que tem seus lados tão pequenos e iguais que são indistinguíveis dos círculos perfeitos. Os círculos puros são os altos sacerdotes. A mulher em Flatland não é mesmo um miserável triângulo, elas são apenas linhas, infinitamente menos respeitadas que os círculos sacerdotais. A discussão da terceira dimensão em Flatland é estritamente proibida. A vida do Sr. Square é rompida um dia por uma criatura 3-D chamada Lorde Sphere. Lorde Sphere manifestou-se como um círculo no mundo 2-D, que pôde magicamente mudar de tamanho.
Lorde Sphere desgrudou o Sr. Square do Flatland 2-D e o arremessou para o "spaceland". O Sr. Square vê somente as seções transversais dos objetos 3-D. Coisas aparecem e desaparecem, e mudam de forma rapidamente. Quando o Sr. Square retornou a Flatland, contou aos outros a sua experiência. Ele foi preso e colocado num confinamento solitário, como punição por ter dito aos outros que a terceira dimensão existe.
Para ver o que o ilustre físico Richard P. Feynman escreveu sobre isso no famoso livro "The Feynman - Lectures on Physics" clique aqui
Os anos de 1890 a 1910 podem ser pensados como os anos áureos da 4ª dimensão. Idéias sobre dimensões maiores permearam círculos literários, o avant garde, e o pensamento do público em geral, afetando as tendências da arte, literatura e filosofia.
Alguns historiadores da arte argumentaram que a quarta dimensão crucialmente influenciou o desenvolvimento do Cubismo e do Expressionismo no mundo da arte. Em particular, isto tomou a forma de uma revolta artística contra as leis da perspectiva.
A arte religiosa da Idade Média ficou notável pela sua deliberada perda de perspectiva. Seus quadros estavam cheios de pessoas e vizinhanças planas. Esta arte refletia a visão da igreja de que Deus era onipotente e poderia por isso ver todas as partes do nosso mundo igualmente. Não era necessária a perspectiva para visão de Deus a respeito das coisas. Daí de acordo com a igreja, a arte tinha de refletir o ponto de vista de Deus. Todas s pinturas tinham de ser bidimensionais.
|
Arte da Idade Média: A Tapeçaria de Bayeux |
 |
A arte renascentista era uma revolta contra esta forma restrita de arte. A perspectiva na arte começou então a ser muito mais popular.
| Arte Renascentista: Quadro de Leonardo Da Vinci 'A Última Ceia' |
 |
A arte cubista revoltou-se contra as restrições impostas por aquela perspectiva. A arte de Picasso mostra uma rejeição clara a perspectiva, com faces femininas vistas simultaneamente de vários ângulos. A pintura de Picasso mostra perspectivas múltiplas, como se ela fosse pintada por alguém da 4ª dimensão, capaz de ver todas as perspectivas simultaneamente.
Arte Cubista: Pintura de Picasso 'Retrato de Dora Maar'
Na Europa, nos anos finais de 1800, falar sobre a 4ª dimensão era o que se fazia nas festas e outras reuniões sociais. Eventualmente as idéias da quarta dimensão cruzou o Atlântico e veio para os Estado Unidos. O principal proponente de todas as coisas 4-D era um matemático inglês, de cor, chamado Charles Hinton. Hinton consumiu toda a sua vida adulta obcecado pela popularização e visualização da quarta dimensão. Em 1885 ele foi preso por bigamia, na Inglaterra, e posto em julgamento. Ele ficou preso por três dias. Imediatamente após a isso ele partiu para o Japão, e acabou chegando aos U.S.A. em 1893.
Hinton queria que existisse um nome para se ir de um lado para ao outro na quarta dimensão, simplesmente como:
para frente e para trás
esquerdo e direito
para cima e para baixo
Suas correspondentes palavras construídas para esta quarta dimensão eram ANA e KATA. Se você estivesse indo na direção ana na quarta dimensão então você estaria indo na direção oposta de alguém indo na direção kata.
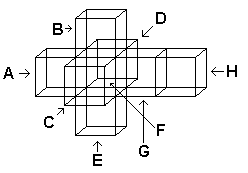
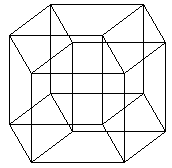
Hinton também foi a pessoa que imaginou um nome para o hipercubo quadrimensional. Ele chamou-o de TESSERATE. Este hipercubo é a generalização do cubo tridimensional. Todos os seus lados devem ser do mesmo comprimento.
Existem três maneiras de se visualizar o Tesserate
(1) O método análogo ao desdobramento.
(2) O método de observar a sombra numa dimensão mais baixa.
(3) O método do fatiamento (i.e., usar seções transversais).
Método 1 Supomha que você tenha de fazer um modelo tal que um Flatlander possa visualizar com que se parece um cubo 3-D. Um modo de fazer isto é desdobrar o cubo e estendê-lo num plano. A criatura 2-D agora seria no mínimo capaz de observar os lados do objeto todo e seria capaz de obter algum sentimento do que ele se parece quando é dobrado de volta para a sua forma usual 3-D. Note que quando a criatura 2-D observa como o cubo é dobrado mais uma vez, ela verá no final somente uma face apenas existente no seu mundo 2-D.
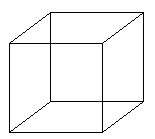 |
 |
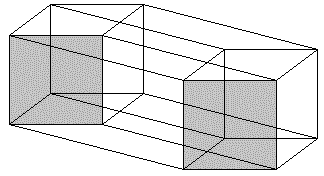
Com que se pareceria um hipercubo desdobrado e estendido no 3-D? Ao invés de se estenderem áreas como foi feito no diagrama acima, seriam, então, estendidos volumes. Simplesmente como as áreas acima são quadrados 2-D, os volumes que emergiriam com um hipercubo desdorado seriam cubos 3-D. A representação de um hipercubo 3-D desdobrado se pareceria com o seguinte objeto.
O hipercubo desdobrado espalha-se num arranjo de oito cubos 3-D. Note que quando dobrado de volta novamente o hipercubo deixa somente um cubo de sobra no nosso mundo 3-D. Esta forma da projeção de hipercubos tem sido feitas em papagaios de papel como mostrado abaixo.
Ela também tem sido mostrada na arte como na pintura feita por Savador Dali mostrada abaixo.
Método 2 Um outro modo de se mostrar com o que parece o cubo 3-D para uma criatura 2-D seria iluminar o objeto para ver como sua sombra se projeta sobre uma superfície 2-D. A criatura 2-D tentaria então inferir da forma da sombra o que o objeto 3-D poderia se assemelhar. Note que existem seis áreas limites no espaço da criatura 2-D, vindas do objeto 3-D. Isto corresponde a seis áreas que estavam presentes no caso desdobrado discutido acima.
 |
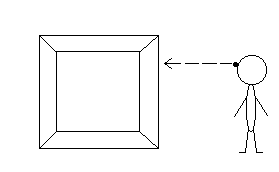 |
Qual é a análoga situação para o hipercubo? Acima existiam 8 volumes. Esperamos que isto ainda seria verdadeiro neste instante. Deveriam existir 8 volumes ressaltados na "sombra" projetada do objeto 4-D num espaço 3-D.

Método 3 A última maneira de mostrar com o que o cubo 3-D realmente se parece para uma criatura 2-D seria fatiar o cubo 3-D em áreas, e dar cada fatia para uma criatura 2-D analisar. Uma fatia de um cubo 3-D é simplesmente um quadrado. Um cubo são muitos quadrados comprimidos todos juntos. Daí qualquer cubo pode ser decomposto em uma seqüência de fatias quadradas.
 |
 |
 |
 |
 |
Uma fatia de um hipercubo será uma generalização da fatia do cubo 3-D. As fatias seria volumes ao invés de áreas.
| Para desenhar a versão fatiada do hipercubo você primeiro desenha dois cubos lado a lado. Daí faça a conexão dos pontos correspondentes de cada cubo. |
 |
 |
Este modelo para os hipercubos foi apresentado primeiramente por Claude Bragdon no seu livro em 1913 "A Primer of Higher Space". Bragdon era um arquiteto que incorporou este e outros modelos 4-D em algumas de suas construções. O edifício da Câmara do Comércio (Chamber of Commerce) em Rochester , New York, é uma de suas construções baseadas nas idéias 4-D.
Para um hipercubo animado clique aqui: HIPERCUBO GIRANTE.
Um bom link para a discussão de estruturas 4-D é http://home.earthlink.net/~bprice/math.html
Críticas às idéias 4-D
Em retrospecto, as idéias de Riemann apresentadas em 1854, foram popularizadas a uma vasta audiência no final ds anos de 1800 e começo dos anos de 1900 por místicos, filósofos e artistas. Nosso entendimento da natureza não foi mensuravelmente aumentado por estas tentativas de analisar dimensões superiores como esperava Riemann.
Não existia tentativas de se usar o hiperespaço para simplificar as leis da natureza.
Nenhuma tentativa foi feita para usar a matemática de Riemann
de maneira aplicada. Ela tornou-se um ramo da matemática pura.
Não existia confirmações experimentais da 4ª dimensão.
Não existiam boas justificativas físicas para a 4ª dimensão; estórias de fantasmas não foram suficientes.
Dentro de poucas décadas do pico de interesse da 4ª dimensão extra do espaço, Einstein relacionou o tempo à 4ª dimensão. Isto mudou a maneira de como as pessoas viam a 4ª dimensão.
Moderno Ressurgimento do interesse em Dimensões Superiores
Em física a dimensão espacial extra foi trazida de volta. Em 1919, Einstein recebeu uma carta de Theodor Kaluza. A carta o surpreendeu porque Kaluza tinha, com sucesso, generalizado a teoria de Einstein da gravidade para cinco dimensões (uma dimensão para o tempo e mais 4 dimensões espacias). O que assombrava Einstein era que adicionando uma dimensão espacial extra Kaluza obteve, não somente a teoria da gravidade, mas também uma teoria do eletromagnetismo. Estas ideias nunca receberam uma atenção maior e ficaram à margem da estrada. Nos anos de 1980, impelido por um desejo de construir uma teoria da natureza que pudesse incorporar todas as forças fundamentais, os físicos ressuscitaram as idéias de Kaluza sobre dimensionalidades superiores, Einstein e outros. Desde então a teoria de dimensões superiores tem se tornado uma ferramenta bem respeitada na tentativa de descrever a natureza numa maneira unificada. Hoje uma das mais respeitadas tentativas de descrever todas as forças fundamentais numa teoria unificada é a chamada Teoria das Supercordas. Esta teoria assume que a maioria das entidades fundamentais são pacotes de energia semelhantes à cordas, a partir das quais todas as partículas fundamentais podem ser construídas. A teoria padrão das supercordas assume que o espaço tem 9 dimensões espaciais e que existe uma dimensão extra para o tempo. Seis das 9 dimensões extras são curvas de raios muito pequenos. Isto supostamente aconteceu muito primitivamente na evoluçao do universo. Por isso, vivemos agora num universo 3-D.
Dimensões e Subsistemas Auto-consistentes
São comuns os argumentos de que somente a vida é 3-D.
Quando a dimensionalidade do espaço é maior do que três, pessoas tem mostrado que formas semelhantes de eletromagnetismo e gravidade existiriam no superior.
Quando a dimensionalidade do espaço é menor do que três dimensões, tem sido argumentado que sistemas neurológicos para qualquer criatura 2-D não seria complexa o suficiente. Os nervos cruzar-se-iam nas nestas criaturas, tornando a transmissão do pensamento muito difícil. O cientista da computação A.K. Dewdney da Universidade de Western Ontario propôs que esta objeção poderia ser contornada pela presença de nós interruptores no cérebro 2-D. Quando um pensamento tem de ser transmitido ele alcança os interruptores através de uma grade de caminhos neurais, cruzados, e é interrompido simplesmente como é feito nos semáforos dos cruzamentos com o tráfego de carros. Um outro problema com as criaturas 2-D é a digestão. Um aparelho digestivo baseado nas criaturas 3-D ficaria cortado em dois pedaços nas criaturas 2-D.
Esta objeção para a vida 2-D, entretanto, pode facilmente ser contornada. Podemos permitir que as criaturas 2-D sejam construídas como alguns platielmintes, que tem somente uma abertura no seu aparelho digestivo. Estas criaturas alimentam-se, e expelem os resíduos, pela mesma abertura. Alternativamente, as criaturas 2-D podem ter um 'auto-controle intestinal'. Cada lado do tubo digestivo teria projeções interbloqueadas. Esta estrutura semelhante a um zíper é aberta na boca quando a criatura se alimenta. Quando a comida passa pelo corpo, o ziper se fecha atrás dos alimentos e se abre à frente dele . O corpo desse modo permanece junto.
Não está claro se os argumentos apresentados sobre vidas de diferentes dimensões estão corrretos, já que eles são de certa forma antropocêntricos. Por que deveriam as estruturas de energia serem as mesmas em universos dimensionalmente diferentes e desarticulados ? Se elas não são as mesmas, então qualquer análise que as pessoas fizessem para mostrar a unicidade do 3-D é falha.