|

|
|
Oh,
pelo amor de Deus, Norman! Você age como se você nunca
tivesse visto um buraco no continuum espaço-tempo anteriormente.
|
As
três propriedades do espaço serão discutidas: Geometria,
Topologia e Dimensionalidade

Geometria
Euclidiana e Geometria Não-Euclidiana
Dentro
de uma área de investigação humana existiu
por muito tempo uma crença calada na nossa habilidade de
examinar a fundo algo da verdade última sobre o universo.
Pessoas pensaram que se este sucesso fosse possível em uma
área de investigação, então talvez ele
também fosse verdade em outras. A fonte desta confiança
era o antigo estudo
da geometria que Euclides
e os gregos antigos tinham colocado em uma firme fundação
lógica.
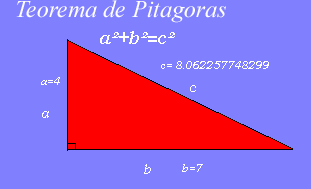 |
A geometria euclidiana
é uma geometria onde o Teorema de Pitágoras para
triângulos é válido. O teorema dá o
quadrado da distância entre dois pontos (c2 no
diagrama) como a soma dos quadrados dos outros dois lados (a2
e b2). Qualquer espaço onde esta distância
euclideana mantén-se válida é dito ser espacialmente
plano.
|
|
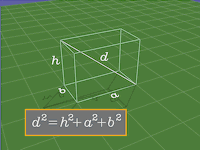
A função-distância
pode ser generalizada a qualquer número de dimensões
espaciais que usam exatamente o padrão que foi usado acima.
No caso 3-D apenas tem que se somar mais uma variável independente.
No diagrama à direita o símbolo h representa esta
nova variável. A variável h é o que nós
normalmente nos referimos como a altura.
|
 |
Geometria
de Euclides tem feito mais do que ajudar os arquitetos e cartógrafos.
Ela tem estabelecido um estilo de raciocínio, dentro do qual
verdades eram deduzidas pela aplicação de regras definidas
de raciocínio de uma coleção de axiomas auto-evidentes.
Teologia e filosofia copiaram este "método axiomático",
e a maioria das formas de argumentos filosóficos seguiram
seu padrão geral. Nos casos extremos, como no trabalho do
filósofo holandês Spinoza, proposições
filosóficas foram mesmo dispostas como as definições,
axiomas, teoremas e provas no trabalho de Euclides.
Era acreditado
que geometria de Euclideana fosse uma descrição de
como era o mundo, ela não era uma aproximação,
ela não era um constructo humano; era a verdade absoluta.
Os teólogos apontaram isto como uma razão para que
as investigações de verdade absolutas fossem legítimas.
No final
dos anos de 1700 Immanuel
Kant , o grande filósofo alemão declarou que a
geometria de Euclides era verdadeira independente da experiência.
No primeiro
quarto dos anos de 1800s as coisas começaram a mudar. A confiança
na geometria de Euclides começava a ser indeterminada. O
famoso matemático Carl
Gauss defendeu que a geometria fosse ditada pelo experimento
(experimento ---> axiomas). Haviam outras geometrias possíveis
descrevendo as interrelações lógicas entre
pontos e linhas sobre superfícies curvas. Estas geometrias
poderiam ter aplicações práticas. Longas distâncias
viajadas sobre a superfície curvada da Terra requeriam geometria
não-Euclidiana.
Por que
as geometrias não-euclidiana não eram tão familiares?
Por que elas eram ainda não familiar? A razão é
que a maioria das pessoas estão restritas à pequenas
porções da superfície da Terra e usualmente
a curvatura da Terra é desprezívelmente pequena nestas
reegiões. Um pedreiro ou um carpinteiro devem usar a geometria
euclidiana, mas um iatista viajando pelo oceano não pode.
|
GLOBAL: Em larga escala,
a curvatura da estru-tura é evi-dente.
|
|
LOCAL: Em peque-na escala,
a curvatu-ra da es-trutura não é facilmente vista.
|
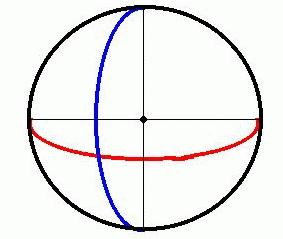
A
curvatura do espaço pode ser classificada em três tipos:
esféria (curvatura positiva), plana (curvatura zero), e hiperbólica
(curvatura negativa).
Na
curvatura esférica os ângulos internos dos triângulos
somam mais do que 180 graus.
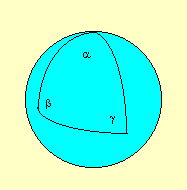
No
espaço plano, os ângulos de um triângulo devem
somar exatamente 180 graus.

Num
espaço hiperbólico os ângulos internos de
um triângulo somam menos do que 180 graus.

Estas
idéias estão resumidas no seguinte diagrama.
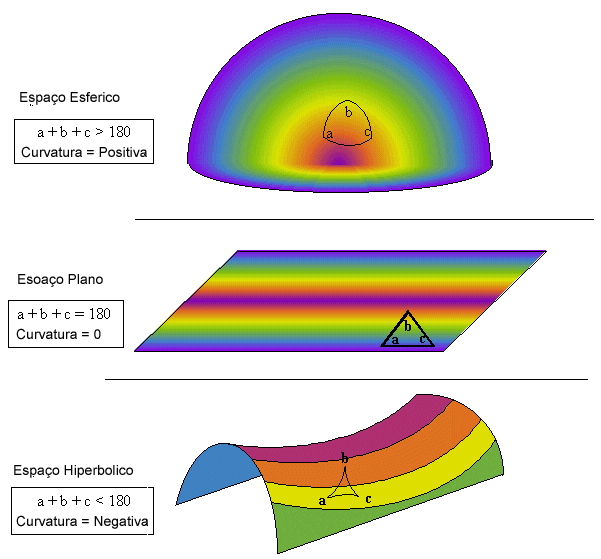
Na
geometria de Euclides todas as superfícies são planas
e linhas paralelas sempre ficam separadas pela mesma distância,
nunca se encontrando e nunca divergindo. Porém, em geometrias
curvas não-Euclideanas, linhas que começam lateralmente
paralelas, eventualmente, cruzam-se uma com a outra, no caso de
curvatura positiva, enquanto estas mesmas linhas divergem uma da
outra, no caso de curvatura negativa. Isto está ilustrado
abaixo para o caso de duas formigas que viajam ao longo dos três
tipos de superfície curvada.

A geometria
do espaço é de grande importância para a cosmologia
pois a Teoria da Relatividade Geral de Einstein,
que será discutida posteriormente, repousa completamente na
idéia de que a geometria do espaço em qualquer local
no universo está relacionada diretamente à intensidade
do campo gravitacional naquele local. Quanto mais forte é o
campo gravitacional, mais forte será, então, a curvatura
associada. Em um contexto cosmológico, os três tipos
de curvatura são
O universo
de curvatura positiva corresponde a um universo que se expandirá
até uma certa separação entre as galáxias
e, daí então, se contrairá de volta até
o espaço zero. Isto é chamado de um universo fechado.
O universo
de curvatura zero corresponde a um universo que expandirá para
sempre, reduzindo a velocidade de expansão à medida
que se expande. Isto é chamado de um universo espacialmente
plano.
O universo
de curvatura negativa corresponde a um universo que se expandirá
para sempre. Isto é chamado de um universo aberto. Para o impresso
de Escher baseado no conceito de curvatura negativa clique sobre a
seguinte figura pequena.


Topologia
Topologia
é o ramo da matemática interessada nas ramificações
de continuidade. Topologistas enfatizam as propriedades das formas
que permanecem inalteradas não importando o quanto as formas
são curvadas e torcidas ou manipuladas de outra forma.
Tais
transformações de objetos idealmente elásticos
estão sujeitos somente à condição que,
para as superfícies, os pontos próximos permanecem
íntimamente juntos no processo de transformação.
Esta condição declara efetivamente ilegal as transformações
que envolvam cortar e colar. Por exemplo, uma rosquinha e uma xícara
de café são topologicamente equivalentes. Uma pode
ser transformada continuamente na outra. O buraco na rosquinha será
preservado como o buraco na alça da xícara de café.
|
Classificação
Topológica
|
|
Objetos
com buracos podem ser classificados topologicamente como
segue:
|
|
Nenhum
buraco
|
Gênero
0
|
|
Um
buraco
|
Gênero
1
|
|
Dois
buracos
|
Gênero
2
|
|
Três
buracos
|
Gênero
3
|
|
EXEMPLOS
|
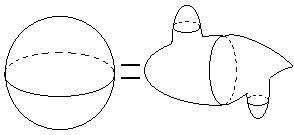 |
|
As formas acima são
topologicamente equivalentes e são do Gênero
0
|
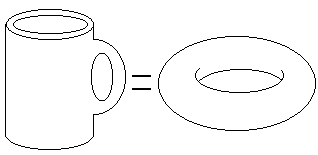
|
|
As formas acima são
topologicamente equivalentes e são do Gênero
1
|
|
Um wormhole (= buraco
de minhoca) é um defeito topológico no espaço
do
gênero 1.
|
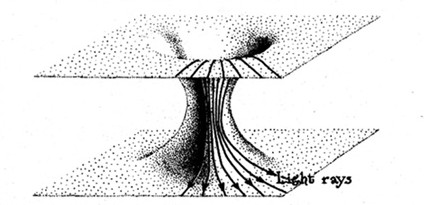 |
Você pode classificar os
seguintes equivalentes topológicos?

Algumas vezes os objetos podem ter o mesmo tipo-gênero
mas eles tem uma torção que os tornam diferentes
topologicamente. Considere a forma de rosquinha doce do gênero-1
mostrada acima e a Moebius
strip (pista de Moebius) do gênero-1 mostrada abaixo.
A Moebius
Strip tem uma torção que permite as formigas
nesta gravura viajarem continuamente ao longo de ambos os lados
da pista.
|
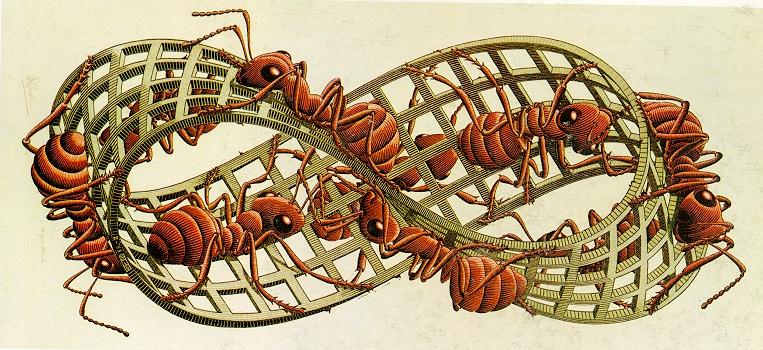 |
Quando esta torção é tomada
no 3-D com a Moebius Strip tornando-se um objeto, o objeto torcido
é chamado de Klein Bottle (=garrafa de Klein). Esta garrafa
é mostrada abaixo numa animação que mostra
como você tem de torcer as coisas para obter o objeto.
|
|
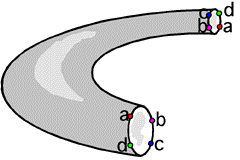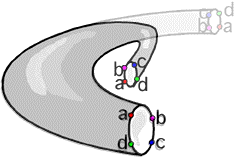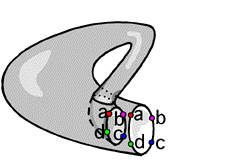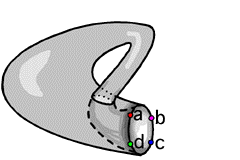
|
Qual
é o significado cosmológico de topologia? A parte
do universo que nós podemos ver é não mais
que 15 bilhões anos luz de raio. Esta parte observável
do universo não mostra nenhum sinal de ter uma topologia
estranha. Porém, nós podemos não ser capazes
de ver as partes cruciais do universo que poderiam conduzir à
observações topológicas interessantes. O diagrama
seguinte dá uma ilustração daquilo que poderia
ser semelhante à observação da topologia cosmológica
O diagrama abaixo
mostra como o espaço pode ser embrulhado num estilo cilíndrico.
|
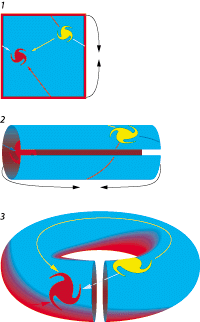 |
Quando o espaço plano que contém
as galáxias é embrulhado em uma forma cilíndrica
e então mais adiante em uma forma de toróide (rosquinhas
doces) as galáxias terão mais de uma maneira para
se "verem" Eventualmente a luz de uma galáxia
alcança a outra pela rota curta e pela rota longa.
|
|
Mais de um modo para "ver"
se traduz na situação onde observadores em galáxias
observam cópias múltiplas cada uma da outra. Esta
é uma predição cosmológica baseada
em considerações de topologia.
|

|
Para ver
como duas estruturas topológicas podem ser feitas com papel,
clique aqui: Topologia
em Modelos de Papel.

|