Uma Introdução à Teoria do Investimento
© William N. Goetzmann
YALE School of Management
Traduzido por L.A. Bertolo
FAFICA - Departamento de Ciências Contábeis
Capítulo III: Preferências e Escolhas do Investidor
O último capítulo apresentou o modelo de Markowitz para seleção
de carteira, mas com um elemento fundamental perdido--escolha da carteira individual.
A fronteira eficiente domina todas as combinações de ativos, porém
ainda tem infinitamente muitos ativos. Como você escolhe uma carteira de
todo o resto como a perfeita para você? Isto mostra ser um grande desafio,
porque exige para os investidores que expressem as suas preferências em
espaço de risco-retorno. Investidores escolhem carteiras por uma miríade
de razões, muito poucos deles podem ser reduzidos a um espaço bidimensional.
Na realidade, os investidores estão acostumados a terem a habilidade de
MUDAREM a decisão de seus investimentos se eles não estiverem se
desenvolvendo como planejado. O modelo de Markowitz simples não permite
esta liberdade. É um modelo de período único, agora usado
amplamente na prática para tomada de decisão em um mundo de multiplos
períodos. Neste capítulo, nós enviaremos alguns dos modos
que se pode aproximar preferências do investidor em espaço de média-variança,
porém estes métodos são somente aproximações.
I. Escolhendo Uma Única Carteira
Como poderia você escolher uma única carteira entre todas aquelas
sobre a fronteira eficiente? Uma aproximação é modelar
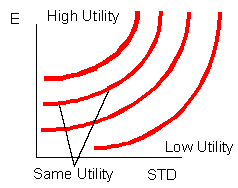
as preferências do investidor matematicamente, usando as curvas de
i so-utilidade. Estas curvas expressam o trade-off risco-retorno para investidores
no espaço bidimensional. Elas funcionam exatamente como linhas num mapa
topológico. Eles são linhas aninhadas que mostram as altitudes
mais altas e mais baixas da região -- excepto que elas medem a altitude
em unidades de utilidade (tudo o que isto é!) em vez de pés ou
metros. Typicamente, uma função matemática conveniente
é escolhida como a base para as curvas iso-utilidade. Por exemplo, poder-se-ía
usar a função logarítmica, ou mesmo parte de uma função
quadrática para capturar a essência das preferências do investidor.
A característica essencial da função é que ela deva
permitir as pessoas demendarem níveis sempre crescentes de retornos ao
assumir mais riscos.
Embora a matemática das funções de utilidade esteja além
do escopo deste curso, se você está interessado em investigações
posteriores, Eu recomendo visitar o Campbell
Harvey's Pages on Optimal Portfolios.
Um modo para caracterizar as diferenças da aversão ao risco do
investidor está na curvatura das linhas de iso-utilidade. Abaixo são
curvas representativas para quatro tipos diferentes de investidores: Um mais
avesso ao risco, um moderadamente avesso ao risco, um menos avesso ao risco,
e um investidor amante do risco. O conjunto todo das curvas aninhadas é
omitido para manter a figura simples.
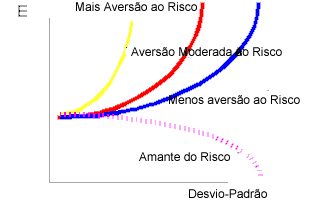 Note que os amantes do risco demandam retornos esperados mais baixos quando o risco aumenta para amnter o mesmo nível de utilidade. Por outro lado, para o investidor mais avêsso ao risco, quando a volatilidade crescer, ele ou ela demandará retornos esperados severamente maiores para manter o portfolio. Estas curvas diferentes resultarão em escolhas diferentes de portfolio para os investidores. O procedimento de otimização simplesmente toma a fronteira de eficiência e encontra o seu ponto de tangência com a curva iso-utilidade mais alta no conjunto investidor. Em outras palavras, ela identifica o único ponto que fornece ao investidor o maior nível de utilidade. Para indivíduos avêssos ao risco, este ponto é único.
Note que os amantes do risco demandam retornos esperados mais baixos quando o risco aumenta para amnter o mesmo nível de utilidade. Por outro lado, para o investidor mais avêsso ao risco, quando a volatilidade crescer, ele ou ela demandará retornos esperados severamente maiores para manter o portfolio. Estas curvas diferentes resultarão em escolhas diferentes de portfolio para os investidores. O procedimento de otimização simplesmente toma a fronteira de eficiência e encontra o seu ponto de tangência com a curva iso-utilidade mais alta no conjunto investidor. Em outras palavras, ela identifica o único ponto que fornece ao investidor o maior nível de utilidade. Para indivíduos avêssos ao risco, este ponto é único.
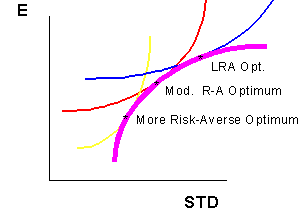
O problema com a aplicação desta metodologia para identificar portfólios ótimos é que ela é difícil para compreender os indivíduos ou instituições avêssos ao risco. Apenas como mapear um terreno desconhecido, os alocadores de ativos deve tentar mapear as estruturas de preferências -- nunca sabendo mesmo se consistente de um dia para outro!
II. Uma outra Aproximação: Preferências sobre Distribuições
O modelo de Markowitz é uma maneira elegante de descrever as diferenças em distribuições de retornos entre portfolios. Uma abordagem para o problema de seleção de portfólio é escolher políticas de investimentos baseada na probabilidade de massa na cauda inferior do lado esquerdo. Este é o chamdao critério short-fall. Sua simplicidade tem um grande apelo. Ele não requer um mapeamento topológico completo das preferências do investidor. Em vez disso ele somente exige que o investidor especifique um retorno mínimo, abaixo do qual ele ou ela queira evitar de cair. A abordagem short-fall escolhe um portfolio na fronteira de eficiência que minimiza a probabilidade do retorno cair abaixo daquele mínimo. Suponha, por exemplo, o seu nível de retorno mínimo especificado seja igual à taxa sem risco, Rf. Para cada portfólio na fronteira, você calcula a razão:
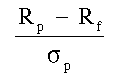
Note que o critério shortfall é como uma t-statistic, onde quanto maior o valor, maior a probabilidade. O portfolio que tiver a maior probabilidade de exceder Rf é aquele para o qual este valor é maximizado. De fato, a similaridade à t-statistic extende mais ainda, como veremos.
Outra coisa útil que ela esclarece é que é bem simples encontrar o portfolio que maximiza a probabilidade de exceder o floor. Você pode fazê-lo graficamente!
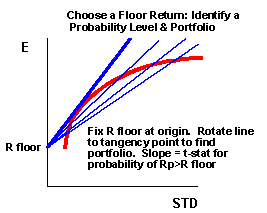
Identificar o nível de retorno floor no eixo Y. Daí então encontrar o ponto de tangência para a fronteira eficiente. Na figura, por exemplo, o ponto de tangência minimiza a probabilidade de se ter um retorno que caia abaixo do
R floor. Um valor floor particular é de interesse -- isto é o floor dado pela taxa sem risco, Rf. A inclinação da linha short-fall quando Rf é o floor é chamada de Índice Sharpe. O portfolio com o máximo Índice Sharpe é aquele que na economia minimiza a probabilidade de cair abaixo dos treasury bills. Da mesma maneira, é aquele portfolio que na economia tem a máxima probabilidade de fornecer um prêmio justo! Isto é, if you must apostar num portfolio para apostar t-bills no futuro, a tangência do portfolio encontrada via o Índice Sharpe será ele.
A abordagem "safety-first" é bem versátil. No exemplo acima, maximizamos a probabilidade de exceder um floor maximizando a inclinação, identificando um ponto de tangência. Você pode também encontrar portfolios por outros métodos. Por exemplo, você pode verificar a possibilidade de um desejável floor e probabilidade de exceder aquele floor fixando o intercepto Y e fixando a inclinação. Either the
ray will pass through the feasible set, or it will not. If it does not, então não existe portfólio que atinja o critério que você especificou. Em caso afirmativo, então existem muitos tais portfolios, e tipicamente aquele um com o maior retorno esperado é aquele que é escolhido.
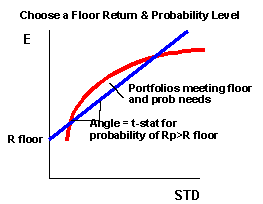 Ontra abordagem é encontrar um floor que coincida com suas necessidades de probabilidade. Em outras palavras, você pergunta "Que retorno floor devo especificar que me dará um nível de confiança de 90% de que o excederei?" Isto é equivalente a configurar a inclinação igual ao valor t-statistic coincidir com o nível de probabilidade. Como isto é equivalente a um teste de uma cauda, você deveria configurar a inclinação para 1.28 (i.e. o quantil da distribuição normal que lhe dá 90% para a esquerda, ou 10% no lado direito da distribuição. Para uma chance de 95%, você deveria escolher uma inclinação de 1.644. Para uma chance de 99% você deverá escolher uma inclinação de 2.32.
Ontra abordagem é encontrar um floor que coincida com suas necessidades de probabilidade. Em outras palavras, você pergunta "Que retorno floor devo especificar que me dará um nível de confiança de 90% de que o excederei?" Isto é equivalente a configurar a inclinação igual ao valor t-statistic coincidir com o nível de probabilidade. Como isto é equivalente a um teste de uma cauda, você deveria configurar a inclinação para 1.28 (i.e. o quantil da distribuição normal que lhe dá 90% para a esquerda, ou 10% no lado direito da distribuição. Para uma chance de 95%, você deveria escolher uma inclinação de 1.644. Para uma chance de 99% você deverá escolher uma inclinação de 2.32.
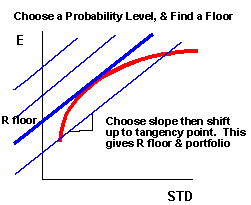
Uma vez escolhida a inclinação, então mova a linha verticalmente até ela se tornar uma tangente. Isto lhe dará ambos, uma floor e uma escolha de portfólio.
III. Uma Nota sobre Value at Risk
A abordagem safety first pode ser usada para calcular o value-at-risk do portfolio. Value-at-risk é uma medida popular crescente do potencial para perda sobre um dado horizonte de tempo. Ele é aplicado no setor bancário para calcular exigências de capital, e é aplicado no setor de investimentos como um controle de risco para portfólios de títulos.
Considere o problema de estimar quão grande seu portfólio poderá experimentar no próximo mês. Se a distribuição dos retornos do portfolio for normal, então cair num desvio padrão três é
possível, mas não muito provável. Geralmente, a estimativa da máxima perda esperada é definida para um dado horizonte de tempo e um dado intervalo de confiança. Considere o tipo de perda que ocorre uma vez em vinte meses. Se você souber a média e o desvio padrão do portfolio, e você especificar o intervalo de confiança como um evento 5% (1 em vinte meses) ou um evento 1% (1 em cem meses) é simples de calcular o "Value at Risk."
Seja Rp o retorno do portf´lio e STDp o desvio padrão do portfólio. Seja T a t-statistic associada com o intervalo de confiança. T de 1.64 corresponde a um em 20 eventos mensais. Seja Rvar o retorno negativo desconhecido do portfolioque esperamos ocorrer um e vinte vezes.
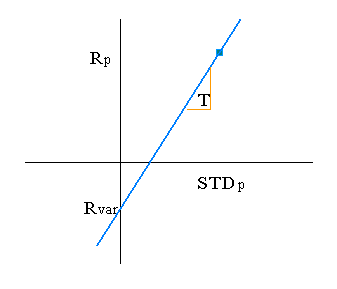
A equação para a linha é: Rp = Rvar + T*STDp e então, Rvar = Rp - T*STDp. Rvar
multiplied times o valor dos ativos no portfolio é o Value at Risk.
Suponha que você esteja considerando o VAR de um portfólio de pensão de $100 milhões durante o horizonte mensal. Ele é composto de 60% ações e 40% de bonds, e você está interessado no intervalo de confiança de 95%.
Vamos assumir que o retorno de ação esperrado mensalmente seja 1% e o retorno esperado do bond seja .7%,
e seus desvios padrões sejam 5% e 3% respectivamente. Assuma que a correlação entre as duas classes de ativos seja .5. Primeiro calculamos a média e o desvio padrão do portfólio:
Rp = (.6)*(.01) + (.4)(.007) = .0088
STDp = sqrt[ .6^2*.05^2 + .4^2*.03^2 + 2*.5*.6*.4*.05*.03] = .038
Então, Rvar = .0088 - 1.64*.038 = -.054
Assim, o value-at-risk mensal do portfólio é ($100 milhões)(.054) = $5.4 milhões.
Note que, a despeito da terminologia, isto realmente não significa que $94.6 não é o risco. A análise somente significa que você espera uma perda no mínimo tão grande quanto $5,4 milhões one month out of 20.
Esta abordagem para se calcular o value-at-risk depende de hipóteses chaves. Primeiro, os retornos devem ser normalmente distribuído. Esta condição é frequentemente violada quando derivativos estão no
portfolio. Segundo, distribuições de retornos historicamente estimadas e correlações devem ser representativas da distribuição de retorno futuro e correlações. O erro de estimação pode ser um grande problema quando você tem estatísticas sobre um grande número de classes de ativos separados a considerar. Terceiro,
retornos não são assumidos serem auto-correlacionados. Qunado existirem tendências positivas nos dados, as perdas deverão ser esperadas crescerem mês a mês.
Em resumo, value at risk está penetrando no setor financeiro como uma medida sumária do risco.
Embroa ela tenha certas desvantagens, sua maior vantagem é que ela é uma abordagem baseada na probabilidade que pode ser vista como uma simples extensão dos modelos de seleção de portfólios safety-first.
IV. Conclusão
Criar uma fronteira eficiente de estatísticas históricas ou projetadas sobre os retornos dos ativos é inerentemente incerta devido a erros nas entradas estatísticas. Estas incerteza é menor quando comparada ao problema de projetar preferências do investidor no espaço média-desvio padrão. Os economistas sabem relativamente pouco sobre as preferências humanas, especialmente quando elas estão confinadas a um modelo de período único. Conhecemos pessoas que preferem mais do que menos, e conhecemos muitas pessoas que evitam o risco quando elas não são compensadas por mantê-lo. Beyond that is guess-work. Não sabemos mesmo se elas são consisteentes, pelo tempo, nas suas escolhas. A abordagem teórica para o problema de seleção de portfólio relies upon specifying uma função utilidade para o investidor, usando isto para identificar as curvas de indiferenças, e daí então encontrar o nível de utilidade mais alto atingível no conjunto possível. This turns out a ser um ponto de tangência. Na prática, é difícil estimar uma função utilidade, e mesmo mais difícil explicá-la de volta para o investidor.
Uma alternativa à estimação da curva de utilidade é a tecnologia "safety-first", que é motivada por uma questão simples sobre preferências. Qual é o seu retorno "floor"? Se você puder escolher um floor, você poderá escolher um portfolio. Além disso, você pode identificar uma probabilidade de exceder aquele floor, observando a inclinação da linha tangente.
Safety-first também leva você a encontrar portfólios otimos escolhendo um floor e uma probabilidade, como também simplesmente picking uma probabilidade.
Value at risk está se tornando um método popular crescente de medida e controle de risco. Ele é uma extensão simples da tecnologia safety-first, quando os ativos componentes do portfólio têm retornos distribuídos normalmente.
IV. Epílogo
Note que a introdução de um título genuino livre de risco
simplifica o problema de carteira para todos os investidores no mundo. Sua escolha
ótima é reduzida ao problema de escolher proporções
de ativos sem risco e o portfolio de risco T (tangência). Os investidores
MRA (More Risk Averse) manteriam um mix de portfolio de tangência e T-bills,
os investidores LRA (Less Risk Averse) tomariam emprestado à taxa sem
risco e investiriam os rendimentos no portfolio tangência.
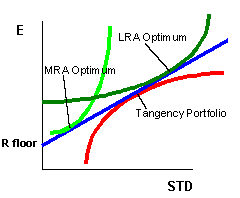
Se pudermos compreender do que o portfolio tangente é composto, poderemos
resolver a decisão de investimento de qualquer um com
o mesmo produto! Do que você pensa que o T é composto? A resposta
está no próximo capítulo.
Para maiores informações sobre a aproximação da
utilidade ao risco, veja a excelente descrição minuciosa de Campbell
Harvey on Optimal Portfolios.. Para um compreensivo hyper-text book sobre
tomada de decisão em, veja William Sharpe's Macro-Investment
Analysis
Barra de Navegação
Capítulo Anterior| Próximo
Capítulo |Will's Home Page|
Menu Principal
de MPPM 540| Tabela de Conteúdos|Mail
Bertolo|
 © William N. Goetzmann
© William N. Goetzmann
YALE School of Management




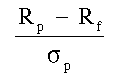





 © William N. Goetzmann
© William N. Goetzmann