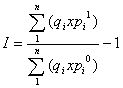INFLAÇÃO
Devemos abordar alguns conceitos relacionados com a inflação, tendo em vista a enorme importância deste fenômeno sobre as operações financeiras realizadas no Brasil. Em contextos inflacionários, deve-se ficar atento para a denominada ilusão monetária, ou rendimento aparente. Nesta situação deve-se determinar a taxa real de juros e o custo ou rendimento real de um financiamento ou aplicação.
1 - INFLAÇÃO E CORREÇÃO MONETÁRIA
A INFLAÇÃO consiste nos aumentos persistentes e generalizados dos preços dos bens e serviços disponíveis à sociedade. O contrário, a diminuição, chama-se DEFLAÇÃO.
A inflação obriga uma quantidade cada vez maior de moeda no pagamento de um bem ou serviço. Sem que tenha havido uma produção maior de riqueza, esse aumento da quantidade de moeda gera perda do poder aquisitivo da própria moeda.
Muitos fenômenos podem causar a inflação. Citam-se, entre eles, taxas altas de juros, escassez, desequilíbrio da balança de pagamentos, emissão de moeda para cobrir déficit público, aumento de preços ou salários sem melhora de qualidade ou de produção, etc.
O processo inflacionário, quando instalado, dificilmente é controlado. Funciona como um círculo vicioso, obrigando a reajustes periódicos de preços e salários, com o seu conseqüente agravamento.
A CORREÇÃO MONETÁRIA tem o objetivo de minimizar ( ou até neutralizar) as distorções causadas pela inflação na economia. Com ela os valores monetários (preços dos bens de serviços, salários, empréstimos, financiamentos, aplicações financeiras, impostos, etc.) são reajustados com base na inflação no período anterior, medida por um índice de preços, que procura medir a mudança que ocorre nos níveis de preços de um período para outro. No Brasil o cálculo deste índice é feito por uma entidade credenciada F.G.V. - RJ (Fundação Getúlio Vargas - Rio de Janeiro), cujos valores nacionais e regionais são publicados na revista Conjuntura Econômica, e pelo I.B.G.E. - Instituto Brasileiro de Geografia e Estatística. Outras instituições também têm elaborado estes cálculos do índices de preços: a FIPE e o DIEESE em São Paulo, a FUNDARJ em Recife, o IPEAD-UFMG em Belo Horizonte
Para comparações específicas e obtenção de taxas reais de crescimento em determinados setores, devem ser utilizados índices de preços particulares de cada setor, por exemplo, construção civil, produtos agropecuários, etc.
O índice mais geral disponível é o Índice Geral de Preço - disponibilidade interna da FGV( IGP-di). É o mais indicado e mede a inflação do país.
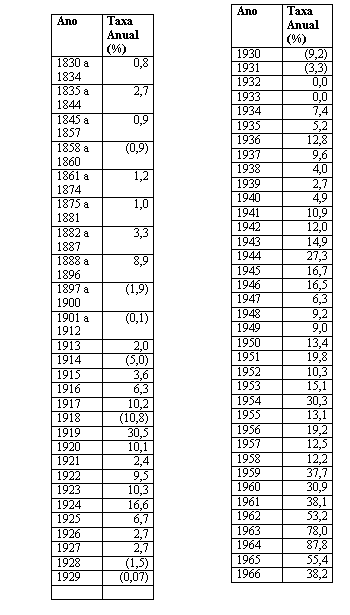
Inflação brasileira no período de 1830 a 2000
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2 - Como representar valores em contextos inflacionários
O processo inflacionário obriga a quem faz cálculo financeiro ou toma decisões de investimento ou financiamento a prestar especial atenção ao significado econômico dos lucros e contas nominais apresentados pelas empresas, ao impacto da inflação na avaliação dos investimentos e como o processo decisório é afetado.
Como resultado da inflação, o significado das medidas contábeis e econômicas de rentabilidade, lucros e custos diverge, e esta divergência é maior à medida que a inflação se acelera. No Brasil, diversos mecanismos foram desenvolvidos para atenuar o impacto da inflação nas peças contábeis das empresas (correção monetária do Balanço Patrimonial, correção integral, etc.) Mas, são mecanismos imperfeitos que aliviam, mas não curam o mal. Enquanto a inflação estiver presente na economia, o tomador de decisões deve saber lidar com ela. Deve-se compreender o significado dos valores nominais, taxas de juros aparentes e reais, custo efetivo aparente e real dos financiamentos, rentabilidade efetiva e real das aplicações, taxas de crescimento nominal e real, atualização monetária e cambial, etc. Nesta seção, auxiliando-nos de exemplos didáticos, iremos introduzir os conceitos e técnicas usados em contextos inflacionários.
EXEMPLO 8
O salário nominal de um operário recebido no último dia de cada mês, nos últimos 3 meses, foi o seguinte:
outubro - R$ 120,00
novembro - R$ 138,00
dezembro - R$ 165,60
Calcular a taxa de crescimento real do salário considerando-se que o índice de preços escolhido teve as seguintes variações:
novembro - 19%
dezembro - 20%
Solução
Para deflacionar(colocar os salários em moeda de outubro), usa-se um “deflator” que assume o valor 1,0000 em outubro. Em novembro, seu valor será 1,000 x 1,19 = 1,1900 e, em dezembro, 1,1900 x 1,22 = 1,4518.
| Final do Mês |
Salarios em valores nominais (1) |
Variação do Índice (2) |
Deflator - base de outubro (3) |
Salário Deflacionado(preços de OUT) (1)/(3) |
Taxa de Crescimento real (% a.m.) |
Taxa de crescimento aparente (% a.m. |
| OUT |
120,00 |
- |
1,0000 |
120,00 |
- |
- |
| NOV |
138,00 |
19% |
1,1900 |
115,96 |
-3,36% |
15%[1] |
| DEZ |
165,60 |
20% |
1,4518 |
114,06 |
-1,64% |
20% |
Com os salários dos 3 meses em moeda do mês de outubro (moeda constante de outubro), pode-se agora, calcular o crescimento real no mês de novembro:
1 + Cr = ![]() Þ Cr = -0,0336 = -3,36%
Þ Cr = -0,0336 = -3,36%
Crescimento real no mês de Dezembro:
Cr = ![]()
Pode-se concluir que em novembro houve perda de 3,36% em termos reais em relação ao mês de outubro e, em dezembro, houve uma perda real de 1,64% em relação ao mês anterior. No período considerado, a perda real foi de 4,95% (taxa real negativa) na capacidade geral de compra do salário:
1 + Cr = ![]() Þ Cr = 0,9505 - 1 = -4,95%
Þ Cr = 0,9505 - 1 = -4,95%
Por outro lado, o crescimento nominal ou aparente mostra taxas de 15% e 20% para os meses de novembro e dezembro. Isto ilustra a importância de trabalhar com valores deflacionados, pois, apenas desta forma, pode-se saber se houve um crescimento acima ou abaixo da inflação.
3 - Taxa de juros aparente e Taxa de juros real
A taxa aparente (chamada nominal nas transações financeiras e comerciais) é aquela que vigora nas operações correntes. Aqui, usaremos a expressão “taxa aparente” para diferenciá-la da taxa nominal (taxa com mais de uma capitalização por período referencial). As taxas reais diferenciam-se das taxas aparentes pela depuração desta dos efeitos da alta geral de preços. As taxas aparente e real relacionam-se da seguinte forma:
(1 + i) = (1 + ir) (1 + I)
onde:
i = taxa aparente ir = taxa real I = taxa de inflação
A taxa real é o rendimento ou custo de uma operação (segundo seja de aplicação ou captação) calculado após serem expurgados os efeitos inflacionários.
EXEMPLO 9
Uma aplicação de $100,00 teve um rendimento de $35,00. Se a inflação do período for de 30%, calcular a rentabilidade aparente e real da operação.
Solução
P = 100,00 I = 30% Rendimento = 35% ir = ? i = ?
Rentabilidade aparente:
i = Rendimento aparente/Aplicação = $35,00/$100,00 = 35%
Rentabilidade Real:
(1 + i) = (1 + ir)(1 + I) Þ ir = ![]() =
= ![]() = 3,85%
= 3,85%
ou detalhadamente
ir = Rendimento real/Aplicação atualizada =
(Montante - Aplicação atualizada)/ Aplicação atualizada =
[(P + rendimento) - P(1 + I)]/P(1 + I) = 3,85%
EXEMPLO 9
Um investimento de $180,00 rende juros e atualização monetária pela inflação do período. Se o rendimento aparente total foi de $45,00 e os juros recebidos foram $20,00, qual a taxa de rentabilidade aparente, qual a taxa de rentabilidade real e qual a taxa de inflação do período?
VER MAIS EXERCÍCIOS NO SAMANEZ pgs 134 a 151
Ver Apostila da Letícia ESALQ
3 - Construção de um indexador e sua utilização
Vamos tomar como exemplo o cálculo do valor do BTN, criado em fevereiro de 1989 e extinto em fevereiro de 1991. Esse indexador foi construído com base na variação mensal dos preços ao consumidor, calculado pelo IBGE. Para os cinco primeiros meses, de fevereiro até junho, essas variações foram, respectivamente, de 3,60%, 6,09%, 7,31%, 9,94%, 24,83%. Seu valor inicial, na data de 01/02/89, foi fixado em NCz$ 1,00 (um cruzado novo). Para a obtenção do valor do mês seguinte, adicionou-se a variação de 3,60% do me de fevereiro, obtendo-se NCz$ 1,0360; o valor do BTN de abril foi obtido adicionando-se 6,09% ao valor do mês anterior e assim sucessivamente. Com esse procedimento, obtém-se os seguintes valores para os cinco primeiros meses de nosso exemplo, válidos para o primeiro dia de cada mês:
| O quadro mostra que o valor do BTN se constituía, na verdade, num índice de preços, como também se constituíam, no passado, a ORTN, a OTN e o fator acumulado da TR; atualmente, temos como exemplos a UFIR, a UPF (Unidade Padrão de Financiamento) e as Unidades Fiscais dos estados e municípios. |
| Mês |
Variação mensal(%) |
BTN |
| Fevereiro/89 |
3,60 |
1,0000 |
| Março |
6,09 |
1,0360 |
| Abril |
7,31 |
1,0991 |
| Maio |
9,94 |
1,1794 |
| Junho |
24,83 |
1,2966 |
A utilização de um índice de preços, isto é, de um indexador, é uma prática generalizada no Brasil. A partir de seus valores, obtém-se facilmente a variação dos preços ocorrida entre duas datas quaisquer, ou o valor atualizado de um empréstimo, de uma aplicação financeira ou de um bem ou serviço. Para a obtenção da variação, basta dividir o índice referente à data atual pelo índice correspondente à data anterior (a partir da qual se pretende determinar a variação), e subtrair 1. Assim, no caso de nosso exemplo, a variação de 1º de março a 1º de junho é calculada como segue:
variação = ![]() -1 = 0,2515444 ou 25,15444%
-1 = 0,2515444 ou 25,15444%
Essa variação corresponde às variações acumuladas dos meses de março, abril e maio.
Para se corrigir monetariamente um valor, ou seja, incorporar ao preço inicial a variação correspondente à inflação do período, basta dividir esse valor pelo índice correspondente à data do início do período (a partir da qual se pretende corrigir) e multiplicar pelo índice referente à data do fim do período. No caso do exemplo anterior, um valor inicial de $ 100.000,00 seria corrigido como segue:
Valor Corrigido = ![]()
A partir deste exemplo, podemos apresentar uma fórmula genérica para atualização monetária de valores e que será utilizada ao posteriormente. Para tento, vamos chamar de principal o preço inicial de uma mercadoria ou serviço, ou o valor inicial de um empréstimo ou seja de uma aplicação financeira, e de indexador qualquer índice utilizado com a finalidade de corrigir monetariamente um valor. A fórmula é a seguinte:
Pc = ![]()
em que Pc é o principal corrigido, P o principal inicial, I0 o indexador correspondente à data inicial (data do contrato) e Iv o indexador da data do vencimento, pagamento ou resgate.
Nos casos em que somente a variação do indexador é conhecida, a atualização se fará como segue:
Pc = P x (1 + V1) x (1 + V2) x (1 + V3) x ..........x (1 + Vn)
em que V representa a variação (diária, mensal ou anual) do indexador e os índices 1, 2, 3, 4, 5, .....,n, o número de ordem do período unitário (dia, mês ou ano)
ESALQ
1.1 – NOÇÕES BÁSICAS
|
Dentre os principais problemas que a inflação ocasiona a uma economia estão o crescimento diferenciado dos preços. O qual beneficia uns e prejudica outros, e o aumento dos custos de transação determinado pelas distorções que o processo inflacionário ocasiona ao sistema de preços.
Mede-se a inflação através de indicadores ou índices que tentam refletir o aumento de preços de um setor em particular ou de um segmento de consumidores. Efetivamente, existem diversos índices que são calculados para o atendimento a várias finalidades.
Os índices de preços ao “consumidor” tentam medir a inflação média de um conjunto de produtos e serviços que se pressupõe sejam os adquiridos por um consumidor com determinadas características de renda. O “índice 2” da Fundação Getúlio Vargas é um dos índices desenvolvidos com a finalidade de medir a inflação de um modo geral, sendo calculado pela média ponderada de índices de preços “ao consumidor”, preços “ao atacado” e preços da “construção civil”.
Para uma melhor visualização do processo de obtenção de índices, será ilustrada, a seguir (Tabela 1.1), a obtenção de um índice de preços para um consumidor hipotético cuja família consome em média 10 kg de arroz, 5 kg de feijão, 5 latas de óleo de soja, 5 kg de carne bovina, 3 litros de leite e 60 passagens de ônibus por mês. Esse conjunto de produtos e serviços (muito maior no caso de índices reais) é denominado “cesta de mercado”, sendo obtido de estudos estatísticos que visam estimar o consumo de produtos em nível domiciliar.
| Mês 0 |
Mês 1 |
|||||
| Produto |
Quantidade |
Preço |
Sub-Total |
Preço |
Sub-Total |
|
| Arroz |
10 kg |
4,00 |
40,00 |
4,30 |
43,00 |
|
| Feijão |
5 kg |
7,00 |
35,00 |
7,80 |
39,00 |
|
| Óleo |
5 latas |
3,00 |
15,00 |
3,30 |
16,50 |
|
| Carne |
5 kg |
2,50 |
12,50 |
3,20 |
16,00 |
|
| Leite |
3 litros |
0,70 |
2,10 |
0,85 |
2,55 |
|
| Passagens |
60 |
0,50 |
30,00 |
0,65 |
39,00 |
|
|
|
134,60 |
156,05 |
||||
| Índice |
100,00 |
115,94 |
||||
Para determinação mensal do valor do índice são levantados os preços dos vários produtos e serviços que compõem a “cesta”, sendo calculado, a seguir, o orçamento necessário para aquisição dos produtos relacionados. A taxa de inflação mensal é obtida pelo cálculo da taxa de crescimento do orçamento de um m~es com relação ao orçamento do mês anterior. Esse processo de obtenção de indicadores resulta no chamado “índice de Laspeyres”, o qual é comumente utilizado. Existem, contudo, outros processos importantes de obtenção de indicadores que não serão discutidos no presente texto, devendo o leitor, em caso de interesse, se reportar à bibliografia recomendada para maiores esclarecimentos.
Objetivamente, o exemplo da Tabela 1.1 mostra que no mês 1 os consumidores necessitavam de R$ 134,60 para adquirir sua “cesta de mercado”, enquanto no mês 2 foram necessários R$ 156,05.
Na última linha da tabela é introduzida a maneira usual de apresentação de um índice,que no caso considera “base” 100 para o mês 0. A idéia associada à base é simples: define-se o número 100 para um determinado mês “base” e acha-se o valor dos índices para os outros meses por regra de três. Neste caso, pode-se perceber que o crescimento dos preços entre duas medidas foi de 15,94%, que representa uma estimativa da inflação para o consumidor considerado, com base nesta “cesta de mercado”.
Se, por exemplo, a variação do índice calculado para correção dos salários dessa pessoa tiver sido de 10%, em lugar dos 15,94% que reflete o aumento de sua “cesta”, isso significaria que ao final do mês 1 essa pessoa estaria comprando menos do conjunto de produtos refletidos em sua cesta. Dessa situação podemos concluir que:
|
Isso significa que a seleção do índice mais apropriado para medir a “inflação” relevante para uma pessoa ou empresa é em si um problema complicado pois não necessariamente os índices disponíveis refletem a variação de preços relevante para cada caso em particular.
A definição formal para taxa de crescimento da inflação entre dois períodos é apresentada a seguir:
|
O procedimento embutido na expressão que acabamos de apresentar para computo da taxa de crescimento da inflação entre dois períodos é chamado de método de Laspeyres, que é o mais comum. É importante, contudo, que o leitor saiba que existem métodos alternativos que utilizam uma cesta de mercado “variável” em lugar da cesta “fixa” usada por Laspeyres.
No exemplo que apresentamos na Tabela 1.1 teríamos:
![]()
Para obtenção da taxa na forma percentual simplesmente multiplicamos por 100 o valor que acabamos de obter. Nessa situação, teríamos então que o índice do exemplo apresentado cresceu 15,94% do mês 0 para o mês 1.
Na grande maioria dos índices calculados por instituições como Fundação Getúlio Vargas ou FIPE – Fundação Instituto de Pesquisas Econômicas, toma-se como “base” um determinado mês de um ano em particular e atribui-se valor 100 ao índice desse mês. Os índices dos outros meses são obtidos por regra de três a partir dos orçamentos em dinheiro necessários para a aquisição da “cesta de produtos” utilizada para cálculo do índice.
|
Se no período 0, o valor do índice for 1100 e no período final (um ano depois por exemplo) ele for 1500, teríamos que a taxa de crescimento da inflação medida por esse índice teria sido de
![]()
ou 36,36% na forma percentual, durante esses períodos.
Freqüentemente é necessário que se proceda a “mudança de base” dos índices de inflação levantados pelas instituições que fazem esse trabalho. Isso significa que o mês utilizado como base 100 para o computo do índice é alterado para um outro mês, em função da alteração da moeda ou em razão de se reduzir o número de dígitos para facilitar o manuseio do índice. Esse procedimento não altera o computo da taxa de crescimento desde que os valores utilizados dos índices sejam provenientes de uma série cujo mês “base” seja o mesmo. A utilização de valores do índice de séries com mês base diferente é uma fonte comum de erro no computo da taxa de crescimento da inflação entre dois períodos.
Apresentamos na Tabela 1.2, valores de índices de inflação comumente utilizados no Brasil. Esses índices são calculados mensalmente através de procedimentos similares aos descritos previamente nesta seção e consideram, cada um deles, uma “cesta” de produtos e serviços diferente. À título de ilustração a taxa de inflação estimada para o mês de julho de 1995 seria dada por 2,24% pelo IGP-FGV, por 3,72% pelo IPC-FIPE e por 4,29% pelo índice calculado pelo DIEESE. Essa dispersão entre as estimativas computadas por procedimentos estatísticos e cestas diferentes ilustram as dificuldades em se estabelecer um índice único de inflação para toda a economia.
Na próxima seção introduzimos os conceitos de “valores nominais” e “valores reais”. Estes conceitos são freqüentemente utilizados em economia e finanças para caracterização de séries históricas de valores monetários.
| Período |
IGP-FGV |
IPC-FIPE |
DIEESE |
| 1990 – média |
0,00226 |
0,00250 |
0,00183 |
| 1991-média |
0,01160 |
0,01126 |
0,01020 |
| 1992 – média |
0,12700 |
0,13400 |
0,11100 |
| 1993 – média |
2,79880 |
2,70820 |
2,39340 |
| 1994 – jan |
12,7827 |
12,1912 |
11,2143 |
| 1994 – fev |
18,2040 |
16,8470 |
15,7111 |
| 1994 – mar |
26,3640 |
23,9126 |
22,8602 |
| 1994 – abr |
37,5574 |
34,9650 |
33,8929 |
| 1994 – mai |
52,9375 |
50,7342 |
49,2740 |
| 1994 – jun |
77,5942 |
76,4818 |
74,2616 |
| 1994 – jul |
96,9678 |
100,0000 |
97,2198 |
| 1994 – ago |
100,0000 |
101,9500 |
100,0000 |
| 1994 – set |
101,5490 |
102,7860 |
100,9593 |
| 1994 – out |
104,1430 |
106,0443 |
104,5379 |
| 1994 – nov |
106,7200 |
109,2469 |
107,6853 |
| 1994 – dez |
107,3250 |
110,6124 |
110,2329 |
| 1995 – jan |
108,7850 |
111,4973 |
113,8313 |
| 1995 – fev |
110,0390 |
112,9691 |
117,1989 |
| 1995 – mar |
112,0350 |
115,1381 |
122,9299 |
| 1995 – abr |
114,6140 |
118,1777 |
128,6627 |
| 1995 – mai |
115,0710 |
120,5058 |
133,2688 |
| 1995 – jun |
118,0900 |
123,7113 |
140,1321 |
| 1995 – jul |
120,7330 |
128,3133 |
146,1438 |