Modelo de precificação binomial com Python
O modelo binomial é um modelo de precificação simples, mas eficaz. Neste artigo, explicaremos a matemática por trás do modelo de precificação binomial, desenvolveremos um script Python para implementá-lo e, finalmente, testá-lo em alguns dados de mercado reais do Yahoo Finance.
Mostraremos também a relação entre o modelo binomial e o famoso modelo Black-Scholes. Consideraremos apenas opções de tipo europeu neste artigo, haverá um artigo futuro focado especificamente em opções de estilo americano. No entanto, os preços das chamadas costumam ser muito próximos, se não iguais, para os vencimentos da UE e dos EUA.
Antes de passarmos para o modelo real, pode ser útil dar alguns exemplos análogos mais simples para explicar a matemática que será usada ao longo deste artigo.
Exemplo
Você é convidado para jogar um jogo no qual uma moeda honesta é lançada n vezes e você recebe $ 1 por cada coroa que sair.
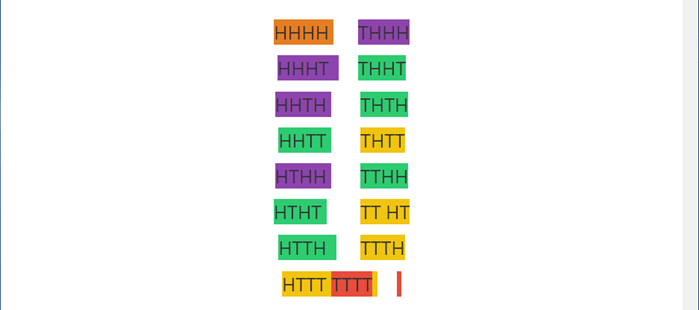
Digamos que joguemos a moeda 4 vezes. Qual é o preço justo para este jogo? Abaixo está uma lista dos 16 resultados possíveis dos 4 lançamentos dados como 2x2x2x2 = 24 os resultados são codificados por cores para representar o mesmo resultado independentemente da ordem, portanto HHHT = THHH

Agora que temos o espaço amostral definido acima. Vamos fazer uma tabela de pagamento lembrando que recebemos $ 1 para cada coroa (H).

O preço justo deste jogo é 0,25 + 0,75 + 0,75 +0,25 = $ 2
O que queremos dizer com preço justo?
Bem, você pode pensar nisso intuitivamente, pois seria neutro sobre se está jogando este jogo ou oferecendo a outra pessoa para jogar este jogo. A razão pela qual você é neutro é que, em média, ao jogar este jogo, você não pode esperar nem ganhar nem perder em média.
Em um jogo dessa natureza, o preço justo e o valor esperado podem ser usados de forma intercambiável. Se oferecido para jogar o jogo pelo preço p para qualquer p<2 você estaria interessado em jogar, pois em média você faria (2−p) $ por jogo jogado. Para preços superiores a 2, você não estaria disposto a jogar, no entanto, estaria disposto a oferecer a outra pessoa para jogar o jogo, pois esperaria ganhar (p−2) $ por iteração do jogo
Agora digamos, por exemplo, que você está oferecendo para jogar este jogo daqui um ano a partir do dia atual. Que preço você estaria disposto a pagar hoje para jogar o jogo daqui a um ano? Ao considerar essas questões, assuma que você pode ganhar 5% depositando seu dinheiro em sua conta poupança.
Bem, podemos pegar o valor esperado que definimos acima e descontá-lo para trás no tempo. Para descontar um pagamento, usamos o V*exp(-rT) onde V é o valor em 1 ano, r é a taxa de juros de 5% neste caso e T é o tempo.
2 * exp(-0,05), aproximadamente $1,90
Estamos assumindo aqui que você é neutro ao risco, pois vê o retorno esperado em um ano exatamente da maneira como vê o retorno de investir em uma conta poupança. Embora neste exemplo artificial, isso possa parecer um pouco estranho, é um conceito útil para entender as opções de preços.
Vamos tentar generalizar o jogo acima, digamos que queremos jogar um jogo em que recebemos $ 1 para cada H acima de algum valor limite. Digamos que jogamos uma moeda n vezes e recebemos $ 1 para cada H maior que algum valor k a fórmula abaixo é a fórmula combinatória.
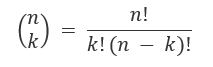
Podemos fazer esta fórmula combinatória em Python como mostrado abaixo. Vamos ver se conseguimos recuperar os H do exemplo acima.
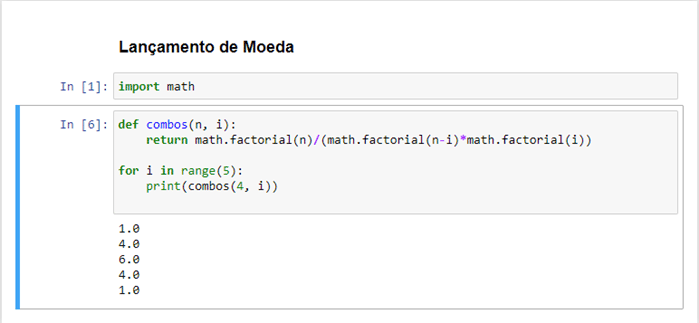
Também podemos recuperar a probabilidade de cada resultado, no exemplo do lançamento da moeda a probabilidade p de cara é 0,5 e k é o número de caras observadas.
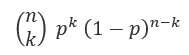
Podemos então encontrar o retorno usando a seguinte fórmula:
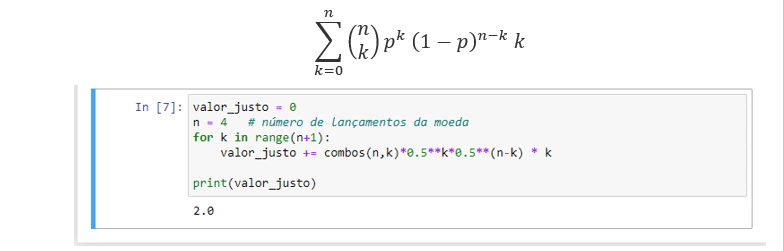
Agora considere se quiséssemos precificar um jogo no qual ganhamos US$ 1 por H acima de um certo limite. Vamos dar um exemplo em que jogamos uma moeda 10 vezes e recebemos $ 1 para cada cara sobre 6.
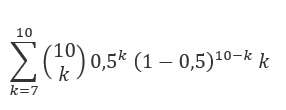
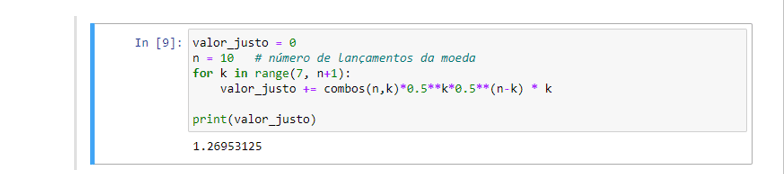
Portanto, embora isso possa parecer um pouco inútil, vamos servir como um exemplo aplicado para introduzir a notação usada no modelo de precificação de opções. Também relacionaremos o lançamento de moedas ao preço real de uma opção.
Preço da opção
Agora que temos alguma intuição sobre como a matemática funciona, aplicaremos os mesmos conceitos à precificação de opções. O modelo de precificação de opções baseado em árvore mais comum conhecido foi criado por Cox, Ross e Rubinstein. Aqui apresentamos o exemplo dado em seu artigo de 1979:
"Suponha que o preço atual de uma ação seja S = $ 50 e, ao final de um período de tempo, seu preço deva ser S * = $ 25 ou S * = $ 100. Uma opção de compra da ação está disponível com um preço impressionante de K = $ 50, com vencimento no final do período. Também é possível tomar emprestado e emprestar a uma taxa de juros de 25%.
Todas as informações, além do preço da chamada, estão disponíveis no extrato acima do jornal. Vamos supor que o tempo de expiração é de 1 ano.
Agora considere formar o seguinte portfólio:
1) Escreva 3 chamadas ao preço C cada
2) Compre duas ações a $ 50
3) Emprestar $ 40 a 25% para ser pago de volta no final do período.
A fim de evitar a arbitragem (lucro livre de risco), a seguinte igualdade deve ser mantida.
3C – 100 +40 = 0
Observe a tabela de retorno para ambos os cenários.
Cenário 1 |
Cenário 2 |
|
| Ação hoje | ST = 25 |
ST = 100 |
| Escreva 3 chamadas ao preço C | - |
-50 * 3 = -150 |
| Compre duas ações por $ 50 | 50 |
200 |
| Emprestar $ 40 a 25% | -50 |
-50 |
| Total | - |
Portanto, o único C que não satisfaz as condições de arbitragem é C = $ 20.
Os autores do artigo passam a mostrar cenários em que o preço C não é igual a 20.
"Se a opção de compra não tivesse o preço de $ 20, um lucro certo seria possível. Em particular, se C = $ 25, o hedge acima renderia uma entrada de caixa atual de $ 15 e não teria mais ganhos ou perdas no futuro. Por outro lado, se C = $ 15, então a mesma coisa poderia ser realizada comprando 3 opções de compra, vendendo a descoberto 2 ações e emprestando $ 40."
O acima é conhecido como um argumento de não-arbitragem para precificação de opções
Vamos introduzir dois termos u e d que denotam movimento para cima e movimento para baixo, respectivamente. Su representa o preço no estado de alta, e Sd representa o preço na baixa (downstate). Anote também o valor p que é representativo da probabilidade neutra ao risco de um movimento ascendente. Deixar r = (1+interest).
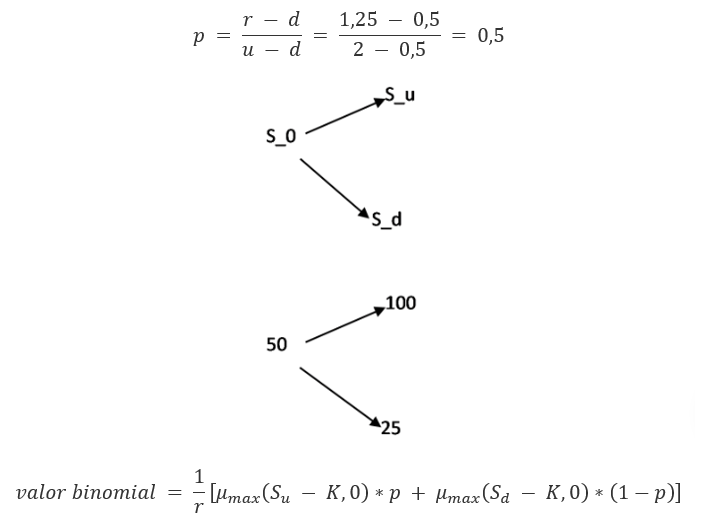
Ligando os números:
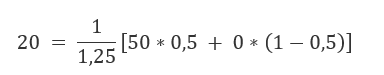
Consulte o exemplo de lançamento de moedas no exemplo mostrado no início do documento, isso pode ser visto no contexto de jogar um jogo de lançamento de moedas em 1 ano.
Determinando o u e d
No exemplo acima, u e d foram dados como 2 e 0,5, respectivamente. No entanto, na prática esses valores não estarão prontamente disponíveis, para estimar esses valores podemos utilizar a volatilidade do ativo. Vejamos outro exemplo em que há uma ação negociada a $ 100, uma opção de compra com preço de exercício de $ 105 e prazo de vencimento de 6 meses. Você estima a volatilidade dos dados históricos em 40%. Digamos que queremos estimar o preço usando 4 etapas em oposição à árvore de uma etapa mostrada acima, para isso precisaremos usar expoentes naturais, pois eles têm a seguinte propriedade exp(uma)*exp(b) = exp(uma+b) isso também é útil para aplicar à taxa livre de risco para representar a composição contínua.

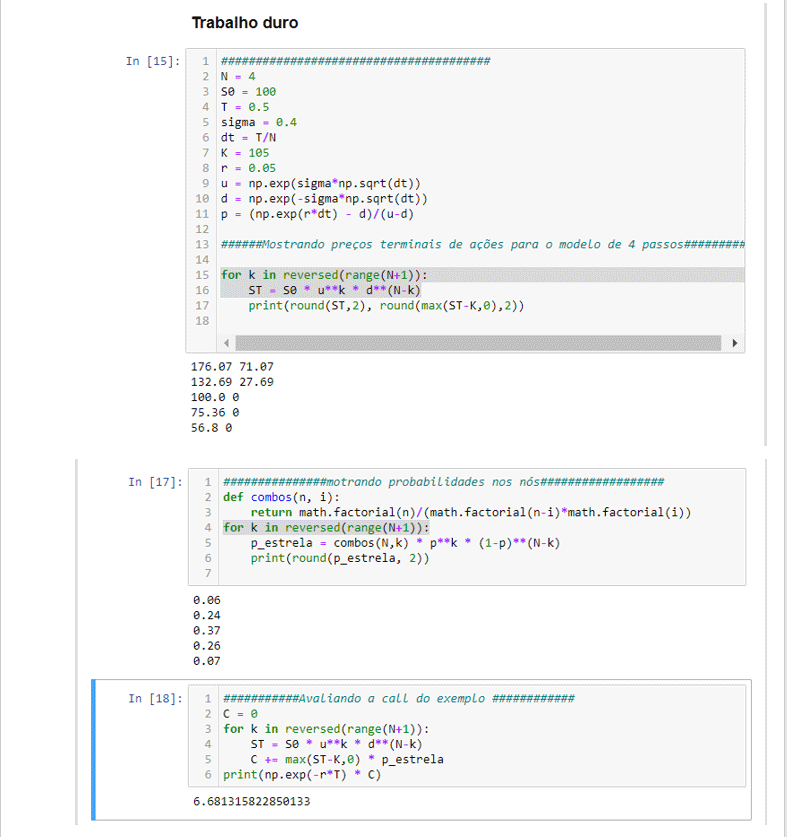
Uma vez que estamos considerando apenas opções europeias que estão disponíveis apenas para exercício no vencimento, os preços das ações terminais serão os mostrados abaixo. Se estivéssemos considerando opções americanas onde a opção de compra pode ser exercida a qualquer momento, precisaríamos considerar os preços em cada um dos intervalos de tempo mostrados no eixo x.
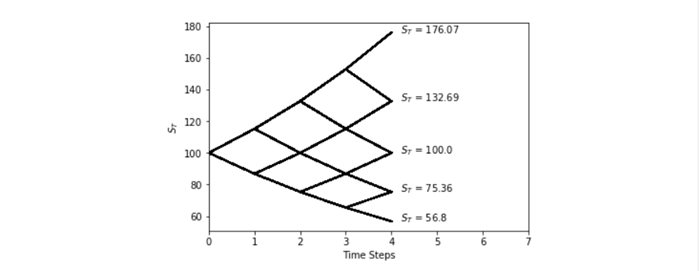
Para obter esses valores em Python, podemos usar o seguinte para obter os preços das ações do terminal e os valores das opções em cada nó.

A probabilidade em cada nó p∗ é dado pelo seguinte. Seja k o número de movimentos ascendentes da ação.

Descobrindo o valor da chamada
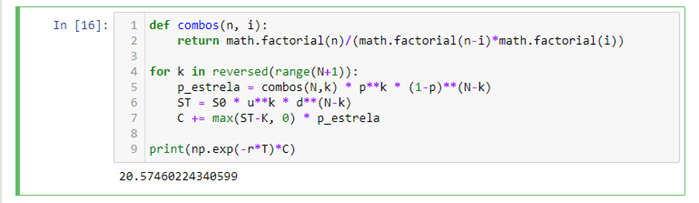
O valor da chamada é então simplesmente uma média ponderada dos valores em cada nó multiplicado pelo valor de probabilidade correspondente.

Vamos colocar o script acima em uma função para que possamos precificar as opções de venda também e aumentar o tamanho do passo Δt facilmente para ver seu efeito no preço da opção.

A função acima está de acordo com o preço que obtivemos da seção de trabalho bruto. Agora podemos aumentar o número de etapas para ver o efeito no preço da chamada.
Observe que, à medida que aumentamos N, o valor da chamada parece convergir para $ 10,22. Este preço é, na verdade, o resultado que obteríamos da fórmula de Black Scholes de forma fechada.
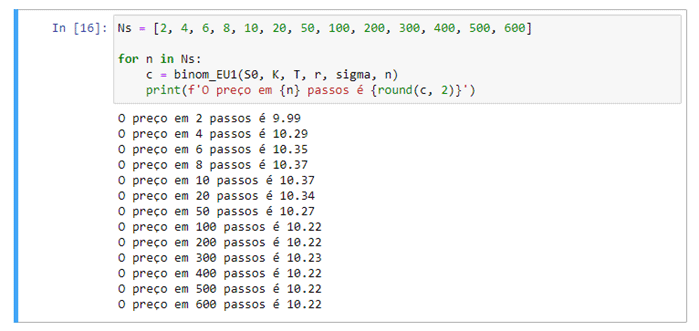
Modelo de opção de lançamento de moedas
Quando falamos de um modelo de opção de lançamento de moeda, considere uma ação que tem um caminho determinado por uma moeda que joga continuamente entre a data atual e a data de vencimento, quando a moeda sai cara a ação sobe e quando sai coroa a ação cai.
Na verdade, o que estamos falando aqui é pegar o limite do modelo binomial como deixamos Δt →0
Considere o que acontece com os parâmetros do modelo quando isso acontece. Bem, vamos perceber que u aproxima-se de 1 pela direita, d se aproxima de 1 pela esquerda e a probabilidade de um movimento para cima (exp(0)-d)/(u-d), então, portanto, isso pode ser representado como um lançamento de moeda.
Vamos considerar um caminho de 100.000 giros para manter iguais os parâmetros do nosso modelo. Novamente, não estamos realmente tomando o limite corretamente aqui, apenas uma aproximação mais próxima, considere fatiar os incrementos no eixo x em incrementos infinitamente pequenos para ter uma ideia do limite real.
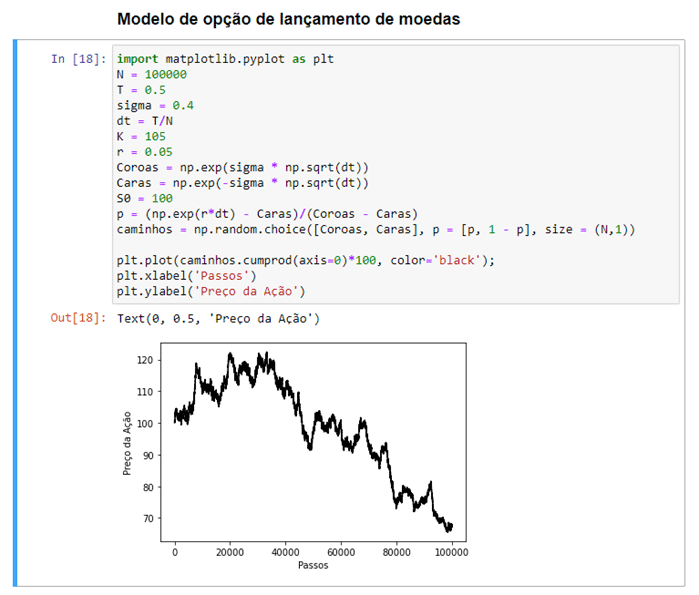
Então, o que isso tem a ver com o modelo binomial? Bem, talvez quando criarmos, digamos, 1000 desses caminhos, fique claro. Note que esta make demora um pouco no seu computador!!!!
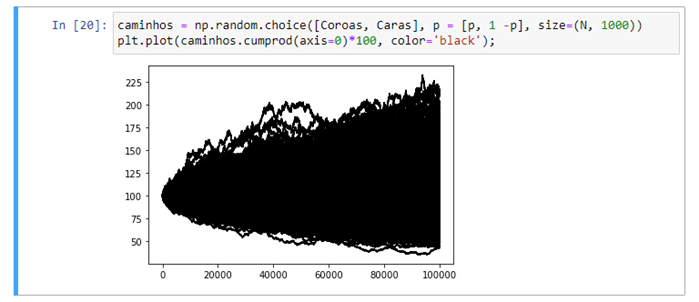
Considere estar na etapa 100.000 acima e pegar os valores terminais do gráfico acima. A recompensa por uma chamada se tornaria então:
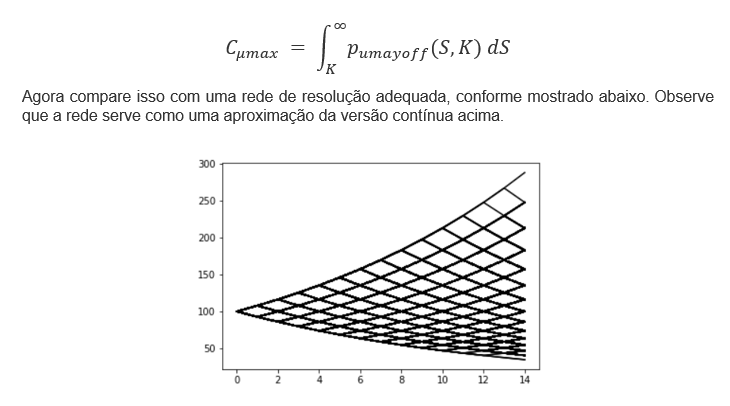
A versão contínua é conhecida como movimento browniano geométrico e, de fato, é exatamente isso que Cox, Ross e Rubinstein estavam aproximando em seu artigo. Claramente, o método de rede fornece uma aproximação precisa do preço se o número de etapas for grande o suficiente.
Precificação de opções reais no Yahoo Finance
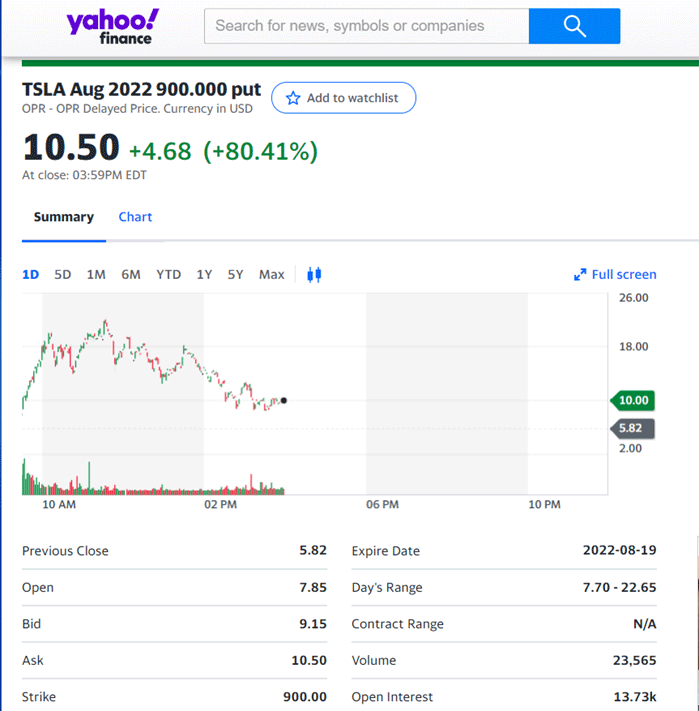
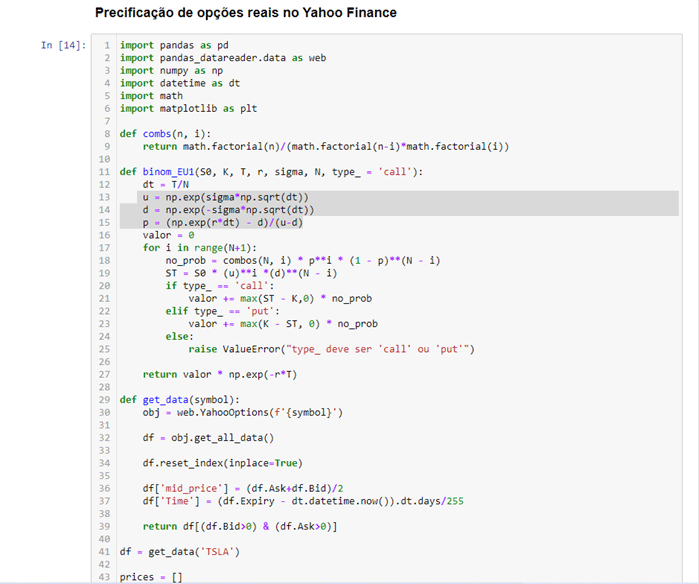
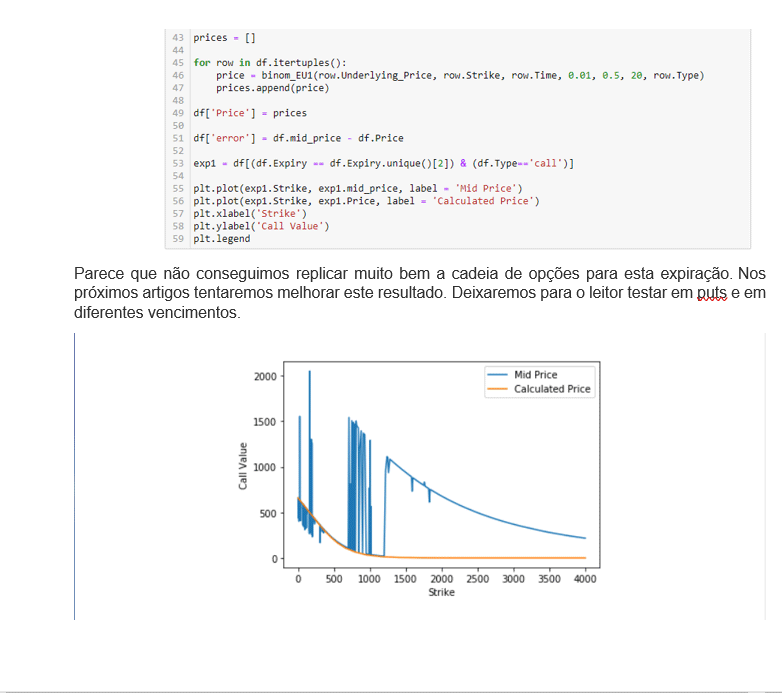
Nesta seção testaremos nosso modelo em dados do Yahoo Finance, mostramos anteriormente como interagir com a API de opções. O problema que provavelmente teremos é que estamos precificando essas opções para TSLA usando um vencimento de opções europeu e as próprias opções provavelmente serão americanas. Também estamos assumindo uma volatilidade constante de 50% (escolhida por conveniência.
Observe que esses dados foram obtidos em 21 de dezembro de 2020. Obviamente, isso mudará se você, o leitor, executar o script novamente.
Bid - é o preço que um comprador está disposto a pagar por um ativo.
Ask - é o preço que um vendedor quer receber para entregar esse ativo.