6.4.4.10. Análise de Box-Jenkins em Dados Sazonais

6. Controle e Monitoramento de Produto ou Processo
6.4. Introdução à Analise de Séries Temporais
6.4.4. Modelos Univariados de Séries Temporais

6.4.4.10. Análise de Box-Jenkins em Dados Sazonais

Série G

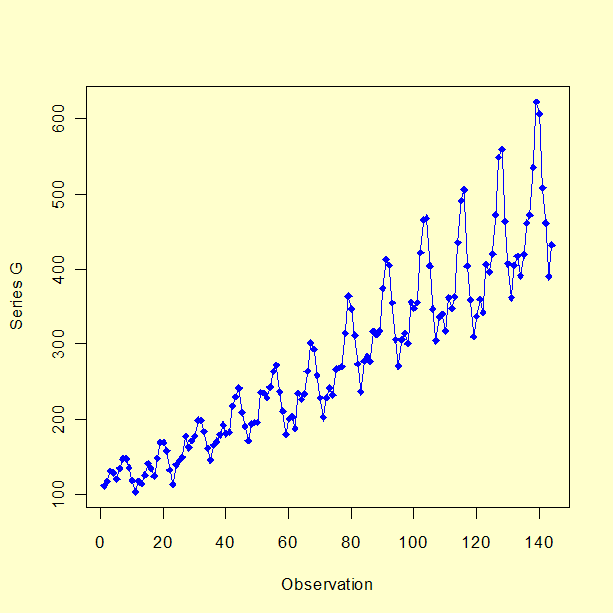
Este exemplo ilustra uma análise de série temporais Box-Jenkins para dados sazonais usando o conjunto de dados da série G em Box, Jenkins, e Reinsel, 1994. Um gráfico das 144 observações está mostrado abaixo. Plot of Series G Data

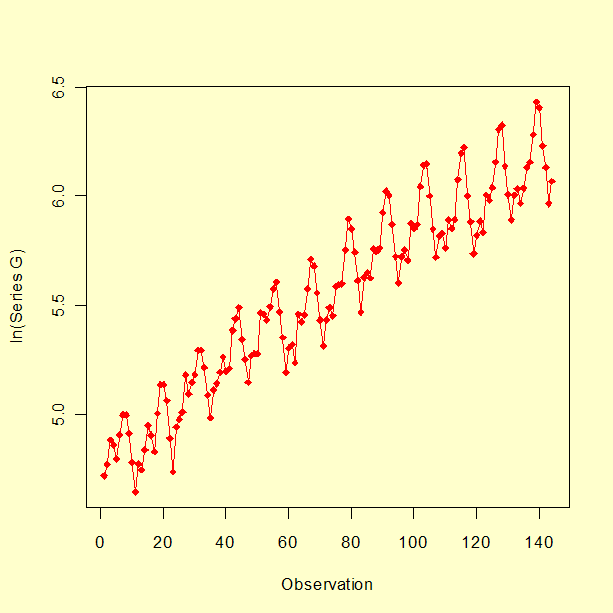
A variância não constante pode ser removida realizando uma transformação logaritmica natural. Plot of natural log of series G

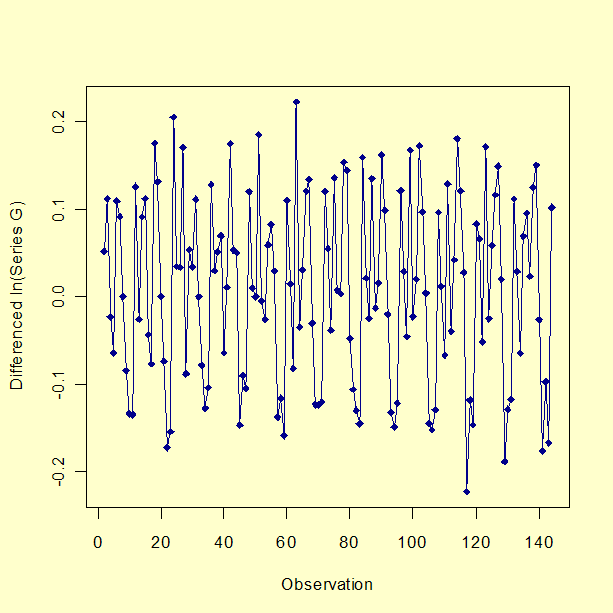
Depois, removemos a tendência na série tomando a primeira diferenciação. A série resultante está mostrada abaixo. Plot of first differences of the natural log of series G

Plot of first differences of the natural log of series G

Analisando o Gráfico de Autocorrelação para a Sazonalidade

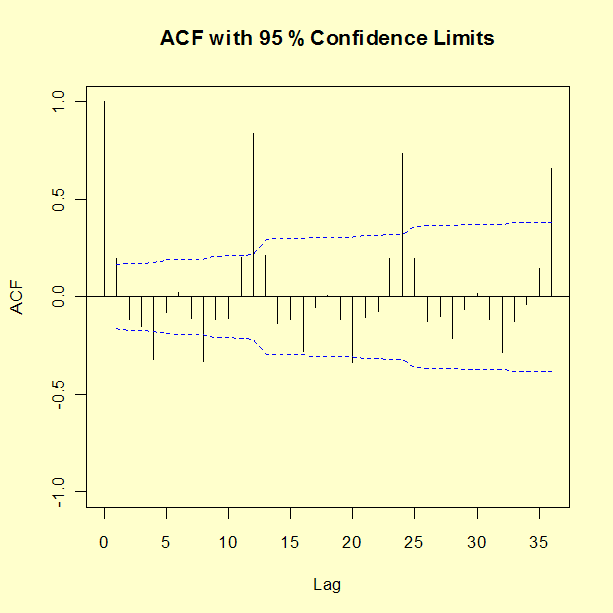
Para identificar um modelo apropriado, plotamos a ACF da série temporal. ACF plot of first differenced natural log series G

Se autocorrelações muito grandes forem observadas em lags espaçados n períodos adiante, por exemplo nos lags 12 e 24, então há evidência de periodicidade. O efeito será removido, pois o objetivo do estágio de identificação é reduzir a autocorrelação por ele. Assim se uma diferenciação simples não for suficiente, tente a diferenciação sazonal num periodo selecionado, tal como 4, 6, ou 12. No nosso exemplo, o período sazonal é 12.

Um gráfico da série G depois de tomar o log natural, primeira diferenciação e diferenciação sazonal está mostrado abaixo.

Seasonal and first differenced natural log of series G

O número dos termos sazonais é raramente mais do que um. Se você souber a forma da sua função de previsão, ou quiser atribuir uma forma particular à função de previsão, você pode selecionar o número apropriado de termos para os modelos AR sazonal ou MA sazonal.

O livro de Box e Jenkins, Time Series Analysis Forecasting and Control (a última edição é Box, Jenkins e Reinsel, 1994) tem uma discussão destas funções de previsão nas páginas 326 - 328. Novamente, se você tiver somente um noção fraca, mas você sabe que existia tendência para cima antes da diferenciação, pegue um termo MA sazonal e veja o que sai no diagnóstico.

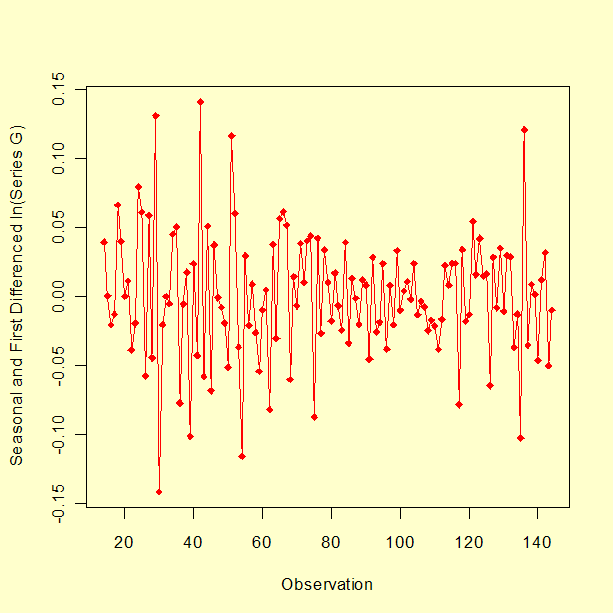
Um gráfico de ACF do log natural da série G com primeira diferenciação e sazonal está mostrado abaixo.

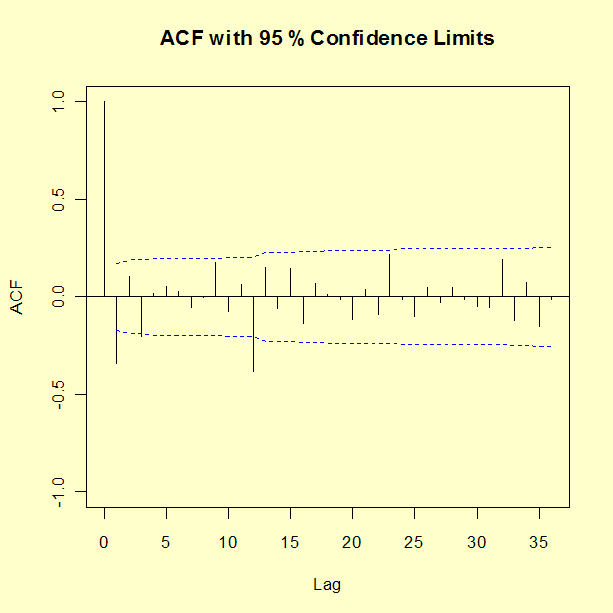
Gráfico da autocorrelação após tomar a diferença sazonal

O gráfico tem oucas estacas, mas a maioria das autocorrelações estão próximas de zero, indicando que o modelo MA(1) sazonal é apropriado.

Ajustando o Modelo

Ajustamos um modelo MA(1) sazonal aos dados

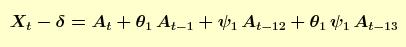
onde θ₁ representa o parâmetro MA(1) e ψ₁ representa o parâmetro sazonal. Os resultados do ajustamento do modelo estão mostrados abaixo.

                            Sazonal
Estimativa            MA(1)     MA(1)
--------          -------    -------
Parâmetro         -0.4018    -0.5569
Erro Padrão        0.0896     0.0731

Desvio padrão residual = 0.0367  
Log da possibilidade = 244.7
AIC = -483.4

Testar a aleatoriedade dos resíduos até 30 lags usando o teste Box-Ljung. Lembre-se que os graus de liberdade para a região crítica deve ser ajustada para levar em conta dois parâmetros estimados.

H₀:  Os resíduos são aleatórios.
H_a:  Os resíduos não são aleatórios.  

Teste estatístico:  Q = 29.4935
Nível de significância:  α = 0.05
Graus de Liberdade:  h = 30 - 2 = 28
Valor Crítico:  Χ²_1-α,h = 41.3371 
Região Crítica: Rejeitar H₀ se Q > 41.3371

Desde que a hipótese nula do teste de Box-Ljung não é rejeitada concluimos que o modelo ajustado é adequado.

Forecasting

Usando nosso modelo MA(1) sazonal, previmos valores de 12 períodos no futuro e calculamos os limites de confiança de 90 %.

              Limite                  Limite
    Período   Inferior   Previsão     Superior
    ------   --------    --------    --------
      145    424.0234    450.7261    478.4649
      146    396.7861    426.0042    456.7577
      147    442.5731    479.3298    518.4399
      148    451.3902    492.7365    537.1454
      149    463.3034    509.3982    559.3245
      150    527.3754    583.7383    645.2544
      151    601.9371    670.4625    745.7830
      152    595.7602    667.5274    746.9323
      153    495.7137    558.5657    628.5389
      154    439.1900    497.5430    562.8899
      155    377.7598    430.1618    489.1730
      156    417.3149    477.5643    545.7760

Gráfico dos valores previstos com limites de confiança de 90%

Todas as análises nesta página podem ser geradas usando R code.