6.4.4.9. Exemplo de Análise de Box-Jenkins Univariados

6. Controle e Monitoramento de Produto ou Processo
6.4. Introdução à Analise de Séries Temporais
6.4.4. Modelos Univariados de Séries Temporais

6.4.4.9. Exemplo de Análise de Box-Jenkins Univariados

Série F

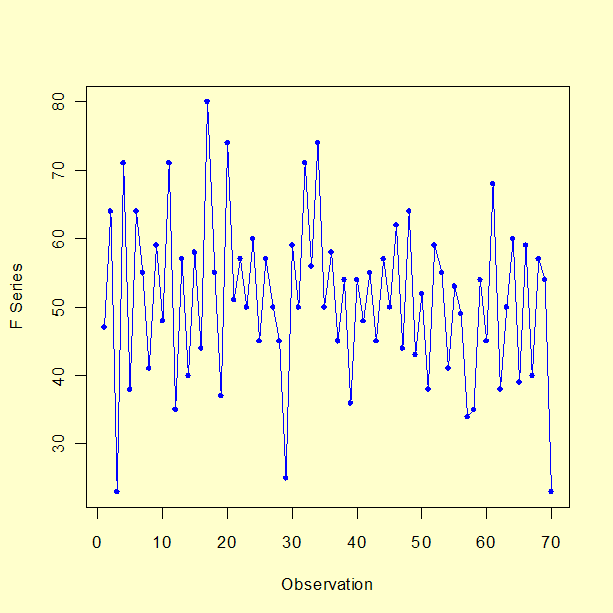
Analisamos conjunto de dados da série F em Box, Jenkins, e Reinsel, 1994. Um gráfico dos 70 pontos de dados brutos é mostrado abaixo. Plot of Series F Data

Os dados não parecem ter um componente sazonal ou uma tendência notável. (A estacionariedade da série foi verificada pelo ajustamento a uma linha reta para os dados versus o período de tempo. A inclinação não foi encontrada ser significativamente diferente de zero (p-value = 0,2).)

Identificação do Modelo

Calculamos a função autocorrelação (ACF) dos dados para os primeiros 35 lags para determinar o tipo de modelo a ajustar aos dados. Listamos os resultados numéricos e plotamos ACF (com limites de confiança de 95 %) versus o número de lag.

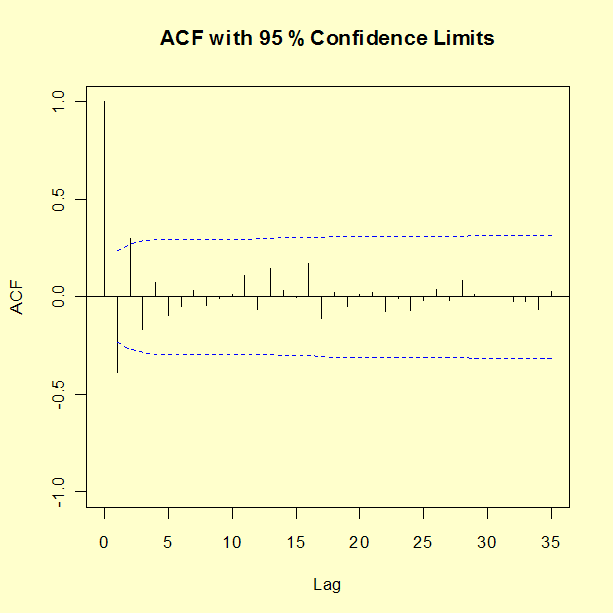
 Lag          ACF
   0  1.000000000
   1 -0.389878319
   2  0.304394082
   3 -0.165554717
   4  0.070719321
   5 -0.097039288
   6 -0.047057692
   7  0.035373112
   8 -0.043458199
   9 -0.004796162
  10  0.014393137
  11  0.109917200
  12 -0.068778492
  13  0.148034489
  14  0.035768581
  15 -0.006677806
  16  0.173004275
  17 -0.111342583
  18  0.019970791
  19 -0.047349722
  20  0.016136806
  21  0.022279561
  22 -0.078710582
  23 -0.009577413
  24 -0.073114034
  25 -0.019503289
  26  0.041465024
  27 -0.022134370
  28  0.088887299
  29  0.016247148
  30  0.003946351
  31  0.004584069
  32 -0.024782198
  33 -0.025905040
  34 -0.062879966
  35  0.026101117

Os valores de ACF se alternam em sinais e decaem rapidamente após o lag 2, indicando que um modelo AR(2) é apropriado para os dados.

Ajustando o Modelo

Ajustamos um modelo AR(2) aos dados.

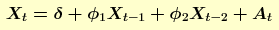
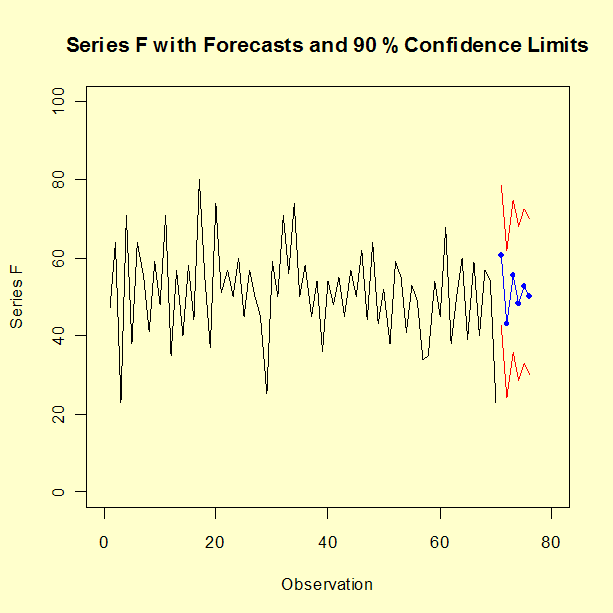
Os resultados do ajustamento do modelo estão mostrados abaixo.

Fonte  Estimativa  Erro Padrão
------  --------  --------------
φ₁       -0.3198      0.1202
φ₂        0.1797      0.1202

δ = 51.1286 
Desvio padrão residual = 10,9599

Teste de aleatoriedade dos resíduos:
Standardized Runs Statistic Z = 0,4887, p-value = 0,625

Previsão

Usando nosso modelo AR(2), projetamos valores para seis períodos no futuro.

Período  Previsão       Erro Padrão
  71      60.6405       10.9479
  72      43.0317       11.4941
  73      55.4274       11.9015
  74      48.2987       12.0108
  75      52.8061       12.0585
  76      50.0835       12.0751

Os dados "históricos" e valores previstos (com limites de confiança de 90 %) são mostrados no gráfico abaixo. Valores previstos do gráfico