6.
Monitoramento e Controle de Processo ou Produto
6.4.
Introdução à Análise de Séries Temporais
6.4.3.
O que é Suavização Exponencial?
6.4.3.5.
|
Suavização Exponencial Tripla
|
|
|
|
O que acontece se os dados apresentarem tendência e sazonalidade?
|
|
Para manusear sazonalidade, teremos de adicionar um terceiro parâmetro
|
Neste caso a suavização dupla não funcionará. Introduzimos agora uma terceira equação que leva em conta a sazonalidade (algumas vezes chamada periodicidade). O conjunto resultante de equações é chamado de método de "Holt-Winters" (HW) que são os nomes de seus inventores.
As equações básicas para o seu método são dadas por:
 onde
onde
- y é a observação
- S é a observação suavizzada
- b é o fator de tendência
- I é o índice sazonal
- F é a previsão em m períodos adiante
- t é um índice denotando um período de tempo
e 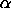 , ,
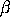 , e , e
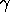 são
constantes que devem ser estimadas de tal modo que o MSE dos erros seja minimizado. Isto fica melhor se deixado para um bom pacote de software. são
constantes que devem ser estimadas de tal modo que o MSE dos erros seja minimizado. Isto fica melhor se deixado para um bom pacote de software.
|
|
Estação completya necessária
|
Para inicializar o método HW precisamos no mínimo dados de uma estação completa para determinar estimativas inciais dos índices de sazonalidade
I t-L.
|
|
L períodos numa estação
|
Dados de uma estação completa consistem de L períodos. E precisamos estimar o fator de tendência de um período para o próximo. Para acompanhar isto, é aconselhável usar duas estações completas, isto é, 2L períodos.
|
|
|
Valores iniciais para o fator tendência
|
|
Como obter estimativas iniciais para os parâmetros de tendência e sazonalidade
|
A fórmula geral para estimar a tendência inicial é dada por
![b = (1/L)*{[(y(L+1)-y(1))/L] + [(y(L+2)-y(2))/L] + ... +
[(y(L+L)-y(L))/L]}](eqns/ts27_new.gif)
|
|
|
Valores iniciais para os Índices de Sazonalidade
|
|
|
Como veremos no exemplo, trabalharemos com dados que consistem de 6 anos com 4 períodos (isto é, 4 trimestres) por ano. Daí então
|
|
Passo 1: calcular médias anuais
|
Passo 1:
Calcular as médias de cada um dos 6 anos
![A(p) = SOMA[i=1 to 4][y(i)]/4 p = 1, 2, ...., 6](eqns/ts28new.gif)
|
|
Passo 2: dividir pelas médias anuais
|
Step 2:
Dividir as observações pela média anual apropriada
|
1
|
2
|
3
|
4
|
5
|
6
|
|
|
y1/A1
|
y5/A2
|
y9/A3
|
y13/A4
|
y17/A5
|
y21/A6
|
|
y2/A1
|
y6/A2
|
y10/A3
|
y14/A4
|
y18/A5
|
y22/A6
|
|
y3/A1
|
y7/A2
|
y11/A3
|
y15/A4
|
y19/A5
|
y23/A6
|
|
y4/A1
|
y8/A2
|
y12/A3
|
y16/A4
|
y20/A5
|
y24/A6
|
|
|
Passo 3: forma dos índices sazonais
|
Passo 3:
Agora os índices sazonais são formados calculando a média de cada linha. Assim os índices sazonais iniciais (simbolicamente) são:
I1 = (
y1/A1 +
y5/A2 +
y9/A3 +
y13/A4 +
y17/A5 +
y21/A6)/6
I2 = (
y2/A1 +
y6/A2 +
y10/A3 +
y14/A4 +
y18/A5 +
y22/A6)/6
I3 = (
y3/A1 +
y7/A2 +
y11/A3 +
y15/A4 +
y19/A5 +
y22/A6)/6
I4 = (
y4/A1 +
y8/A2 +
y12/A3 +
y16/A4 +
y20/A5 +
y24/A6)/6
Sabemos agora a álgebra por detrás do cálculo das estimativas iniciais.
A próxima página contém um exemplo de suavização exponencial tripla.
|
|
|
O caso dos Coeficientes Zero
|
|
Coeficientes zero para os parâmetros de tendência e sazonalidade
|
Algumas vezes acontece que um programa de computador para suavização exponencial tripla fornece coeficiente para tendência
(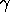 )
ou para sazonalidade
( )
ou para sazonalidade
(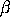 ) zero.
Ou o pior, ambos saem como zero! ) zero.
Ou o pior, ambos saem como zero!
Isto indica que não há tendência e/ou não sazonalidade?
É claro que não! Somente significa que os valores iniciais para tendência e/ou sazonalidade foram corretos no dinheiro. Nenhuma atualização foi necessária para se chegar ao MSE mais baixo possível. Deveríamos inspecionar fórmulas de atualização para verificar isto.
|
 onde
onde
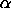 ,
,
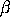 , e
, e
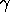 são
constantes que devem ser estimadas de tal modo que o MSE dos erros seja minimizado. Isto fica melhor se deixado para um bom pacote de software.
são
constantes que devem ser estimadas de tal modo que o MSE dos erros seja minimizado. Isto fica melhor se deixado para um bom pacote de software.
![b = (1/L)*{[(y(L+1)-y(1))/L] + [(y(L+2)-y(2))/L] + ... +
[(y(L+L)-y(L))/L]}](eqns/ts27_new.gif)
![A(p) = SOMA[i=1 to 4][y(i)]/4 p = 1, 2, ...., 6](eqns/ts28new.gif)
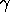 )
ou para sazonalidade
(
)
ou para sazonalidade
(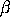 ) zero.
Ou o pior, ambos saem como zero!
) zero.
Ou o pior, ambos saem como zero!

