6.4. Introdução à Analise de Séries Temporais
6.4.3. O que é Suavização Exponencial?
6.4.3.2. |
Previsão com Suavização Exponencial Simples |
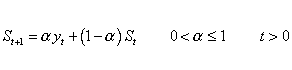
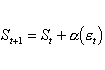
 t é o erro de previsão (real - previsto) para o período t.
t é o erro de previsão (real - previsto) para o período t.
Em outras palavras, a previsão nova é a antiga mais um ajustamento para o erro que ocorreu na última previsão.
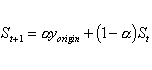
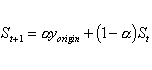
= .1(70) + .9(71.7) = 71.5 (
 = .1)
= .1)
Mas para a próxima previsão não temos ponto de dados (observação). Assim agora calculamos:
| Período |
previsão Bootstrap |
Dados |
Previsão Suavização Simples |
|---|---|---|---|
|
|
|||
| 13 | 71.50 | 75 | 71.5 |
| 14 | 71.35 | 75 | 71.9 |
| 15 | 71.21 | 74 | 72.2 |
| 16 | 71.09 | 78 | 72.4 |
| 17 | 70.98 | 86 | 73.0 |
 não é suficiente.
não é suficiente.
 de 0.3:
de 0.3:
| Dados | Ajuste |
|---|---|
|
|
|
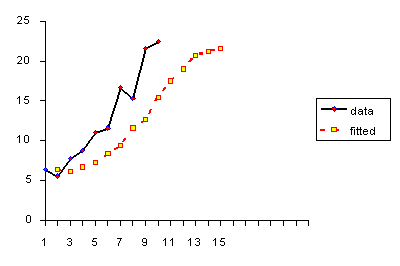
| 6.4 | |
| 5.6 | 6.4 |
| 7.8 | 6.2 |
| 8.8 | 6.7 |
| 11.0 | 7.3 |
| 11.6 | 8.4 |
| 16.7 | 9.4 |
| 15.3 | 11.6 |
| 21.6 | 12.7 |
| 22.4 | 15.4 |