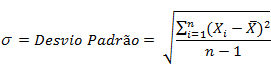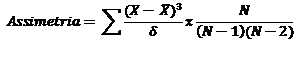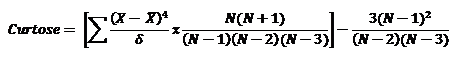Tutorial 02 – Básico de Simulação no VBA do Excel

Este tutorial é a segunda parte da série Tutorial sobre Simulação Básica no VBA do Excel.  Ela  fornece tutoriais do VBA DO Excel sobre como criar estimativas estatísticas que são usadas para analisar os dados de uma simulação.  Muitos dos exemplos usados já estão disponíveis nas funções do Excel.  Os usuários podem usar estas funções do Excel como ferramentas para verificarem seus resultados oriundos dos exemplos.   Estes exemplos exigem habilidades de programação básica em VBA.  Os usuários são estimulados  a lerem o Tutorial 01 sobre o Básico de Simulação no VBA do Excel se eles tiverem problemas de entendimento dos conceitos e termos de programação usados nesta página.

Este documento contém informação sobre os seguintes tópicos.

Números Aleatórios e a Declaração Randomize

Desvio Padrão e Média

Distorção e Curtose

Percentís e Intervalo de Confiança

Lucratividade

Criando um Histograma

Números Aleatórios e a Declaração Randomize

Para gerar números aleatórios de 0 até 1 uniformemente, pode-se usar a função Rand() do Excel ou a função Rnd do VBA.  Estas duas funções são as mães de todos os números aleatórios.  Você precisará de uma destas funções para gerar números aleatórios de quaisquer distribuições de probabilidade.

O exemplo seguinte gera 5 números aleatórios e daí mostra-os numa caixa de mensagem:

Sub rndNo()
    Dim str As String
   
    For i = 1 To 5
        str = str & CStr(Rnd) & vbCrLf
    Next i
   
    MsgBox str   
End Sub

* A função CStr() converte números aleatórios em string.

Até aqui tudo bem. Mas quando fechamos o arquivo, e reabrimos e rodamos a sub-rotina novamente, os mesmos 5 números aparecem! 

A razão do porque isto ocorre é que os números aleatórios foram gerados realmente do mesmo conjunto de números (chamado semente).  Colocando a declaração Randomize na sub-rotina, os números serão gerados de uma nova semente.  (Randomize usa o valor de retorno da função Timer como o novo valor semente.) 

A nova rotina pode ser como segue:

Sub rndNo()
    Dim str As String
   
    Randomize
    For i = 1 To 5
        str = str & CStr(Rnd) & vbCrLf
    Next i
   
    MsgBox str   
End Sub

Algumas vezes desejaríamos usar a mesma semente repetidamente apenas mudando os valores de certas variáveis nas nossas simulações para ver como a mudança afeta o resultado.  Em tal caso, omitimos a declaração Randomize na nossa sub-rotina.


Para mais informação, refira-se ao Help do VBA do Excel no seu programa Excel.

Desvio Padrão e Média

O desvio padrão e a média são duas estimativas estatísticas muito usadas.  O desvio padrão mede o “espalhamento” da distribuição.

O que segue são funções que calculam a média e o desvio padrão.  Estas funções são semelhantes às outras funções usadas nos nossos exemplos: elas tomam arrays como seus argumentos.

Function Media(Arr() As Single)
     Dim Soma As Single
     Dim i As Integer

    Soma = 0
    For i = 1 To UBound(Arr)
        Soma = Soma + Arr(i)
    Next i
 
    Media = Soma / UBound(Arr)
End Function


Function DesvPadrao(Arr() As Single)
     Dim i As Integer
     Dim med As Single, SomaQ As Single
 
     med = Media(Arr)
     For i = 1 To UBound(Arr)
          SomaQ = SomaQ + (Arr(i) - med) ^ 2
     Next i
 
     DesvPadrao = Sqr(SomaQ / (UBound(Arr) - 1))
End Function

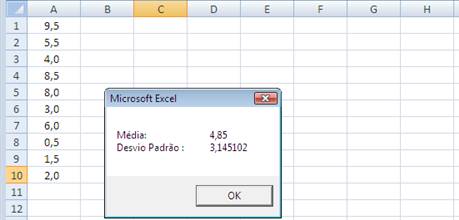
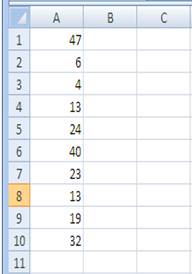
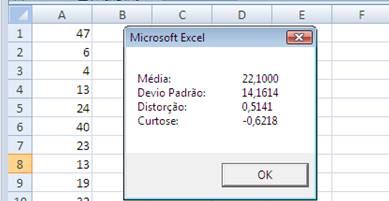
A sub-rotina seguinte lê os dados na coluna um da linha 1 até a linha 10 (da Plan1) no array, chama ambas as funções passando os argumentos a elas, calcula a média (average) e o desvio padrão, e retorna os valores numa caixa de mensagem.

Sub compute()
     Dim Arr(10) As Single
     Dim Average As Single
     Dim Desv_Pad As Single

     For i = 1 To UBound(Arr)
          Arr(i) = Sheets("Plan1").Cells(i, 1)
     Next i

     Average = Media(Arr)
    Desv_Pad = DesvPadrao(Arr)
     MsgBox "Média:" & vbTab & Average & vbCrLf & "Desvio Padrão :" & vbTab & Desv_Pad
End Sub

A figura abaixo mostra os dados e o resultado.

Exemplo semelhante também é usado nos exemplos de Desvio Padrão e Média na seção VBA.


(Estas funções são semelhantes às funções AVERAGE() e STDEV() fornecidas pelo Excel.)    

Distorção e Curtose

Distorção mede o grau de assimetria da distribuição.  Por exemplo, a Distorção de uma distribuição normal é 0 pois uma distribuição normal é simétrica.  Distorção positiva indica uma distribuição com uma  cauda assimétrica estendendo adiante para os valores positivos, enquanto que uma distorção negativa estende adiante para os valores negativos.

Curtose mede o grau de aguçamento ou achatamento de uma distribuição comparada com a distribuição normal.  Uma curtose positiva indica uma distribuição relativamente aguçada.  Uma curtose negativa indica uma distribuição relativamente achatada. 

Freqüentemente, estas duas estimativas juntamente com a média e o desvio padrão são usadas para testar para ver se os dados simulados de uma distribuição são legítimos (se os dados representam a distribuição).

A sub-rotina seguinte, calcule(), lê os dados seguintes numa coluna de 1 até 10 (da planilha ativa) no array,

chama ambas as funções passando os argumentos, calcula os quatro momentos (chamados média, desvio padrão, distorção, e curtose) e retorna os valores numa caixa de mensagem.

Sub calcule()

    Dim arr(10) As Single

    For i = 1 To 10

        arr(i) = Cells(i, 1)

    Next i

    MsgBox "Média:          " & vbTab & Format(MediaA(arr), "0.0000") & vbCrLf & _

    "Devio Padrão: " & vbTab & Format(Var(arr) ^ 0.5, "0.0000") & vbCrLf & _

    "Distorção:         " & vbTab & Format(Distorc(arr), "0.0000") & vbCrLf & _

    "Curtose:       " & vbTab & Format(Curtose(arr), "0.0000")

End Sub

Function Distorc(arr() As Single)

    Dim i As Long, n As Long

    Dim med As Single, dp As Single, SomaAte3 As Single

    n = UBound(arr)

    med = MediaA(arr)

    dp = (Var(arr)) ^ 0.5

    SomaAte3 = 0

    For i = 1 To n

        SomaAte3 = SomaAte3 + ((arr(i) - med) / dp) ^ 3

    Next i

    Distorc = SomaAte3 * (n / ((n - 1) * (n - 2)))

End Function

Function Curtose(arr() As Single)

    Dim i As Long, n As Long

    Dim med As Single, dp As Single, SomaAte3 As Single

    n = UBound(arr)

    med = MediaA(arr)

    dp = (Var(arr)) ^ 0.5

    SomaAte4 = 0

    For i = 1 To n

        SomaAte4 = SomaAte4 + ((arr(i) - med) / dp) ^ 4

    Next i

    Curtose = SomaAte4 * (n * (n + 1) / ((n - 1) * (n - 2) * (n - 3))) - (3 * (n - 1) ^ 2 / ((n - 2) * (n - 3)))

End Function

Function MediaA(arr() As Single)

    Dim Soma As Single

    Dim i As Long, k As Long

    k = UBound(arr)

    Soma = 0

    For i = 1 To k

        Soma = Soma + arr(i)

    Next i

    MediaA = Soma / k

End Function

Function Var(arr() As Single)

    Dim i As Long

    Dim med As Single, SomaQ As Single

    k = UBound(arr)

    med = MediaA(arr)

    For i = 1 To k

        SomaQ = SomaQ + (arr(i) - med) ^ 2

    Next i

    Var = SomaQ / (k - 1)

      End Function

A figura abaixo mostra os dados e o resultado.
                         

(Estas funções são semelhantes às funções DISTORÇÂO() e a CURT() fornecidas pelo Excel.)  

Percentis e Intervalo de Confiança

Percentil retorna o k-ésimo percentil dos valores num intervalo.  Um intervalo de confiança é o intervalo entre dois percentís.  Por exemplo: se um conjunto de dados tem 20 números variando de 2.5 até 50 com um incremento de 2.5 (2.5, 5, ...., 50), o 80º percentil será 40.  Isto significa que 80% dos elementos do conjunto serão iguais ou abaixo de 40.  Se o valor alfa é 10%, para um teste de duas caudas, o percentil inferior deverá ser  5% (alfa/2) e o percentil superior deverá ser configurado para 95% (1 - alfa/2).

Para obter o percentil, os dados precisam ser ordenados.  Na sub-rotina (ObterPercentil()) Abaixo, 10 números aleatórios entre 1 até 50 são atribuídos a um array.  A sub rotina chama a função percentil (u_percentil()).  A função chama a sub-rotina Ordenar para ordenar o array.  A função obtém os valores do array baseado no percentil (40%), e retorna o valor do percentil de volta para a sub-rotina. 

Note que Application.Max(Application.Min(Int(k * n), n), 1) na função percentil garante que primeiro, o índice do array é um inteiro e segundo, o valor máximo e mínimo para o índice de array não excederá o número de elementos no conjunto de dados ou abaixo de 1, respectivamente.

Os dados e os resultados são como segue:

Os números em azul estão abaixo do percentil  40%.  Treze (13), neste caso, é o valor que a função retorna no percentil 40%.

Aqui está o programa completo para o exemplo acima:

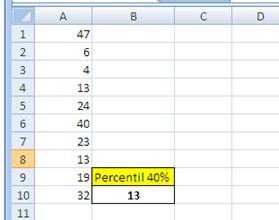
Sub ObterPercentil()

    Dim arr(10) As Single

    For i = 1 To 10

        arr(i) = Int(Rnd * 50) + 1

        Cells(i, 1) = arr(i)

    Next i

    Cells(10, 2) = u_percentil(arr, 0.4)

End Sub

Function u_percentil(arr() As Single, k As Single)

    Dim i As Integer, n As Integer

    n = UBound(arr)

    Call Ordenar(arr)

    x = Application.Max(Application.Min(Int(k * n), n), 1)

    u_percentil = arr(x)

End Function

Sub Ordenar(ByRef arr() As Single)

    Dim Temp As Single

    Dim i As Long

    Dim j As Long

    For j = 2 To UBound(arr)

        Temp = arr(j)

        For i = j - 1 To 1 Step -1

            If (arr(i) <= Temp) Then GoTo 10

            arr(i + 1) = arr(i)

        Next i

        i = 0

10      arr(i + 1) = Temp

        If j Mod 100 = 0 Then

            Cells(26, 5) = j

        End If

    Next j

End Sub

Conceitos similares deste tutorial são usados em muitos de nossos exemplos de simulações.

(Esta função é similar às funções PERCENTIL() e a QUARTIL() fornecidas pelo Excel.)

Lucratividade

O exemplo de percentil anterior mostra como obter o valor que corresponde a um percentil específico. Neste exemplo, mostraremos a você como obter o percentil com um dado valor.

Iniciaremos este tutorial mostrando-lhe uma simulação muito simples.  Entretanto, a simulação não precisa obter a resposta neste exemplo porque estamos usando hipóteses muito fracas.  O resultado pode realmente ser calculado na sua cabeça se sua matemática for boa.

Assuma que os seus lucros estejam distribuídos uniformemente.  Dos registros passados, vocÊ sabe que seu lucro médio anual flutua entre -$100.000 até $500.000.  Queremos saber qual é a lucratividade que você terá com $300.000 no próximo ano mantendo todas as outras coisas constantes.  Bastante interessante?  Agora repare isto:

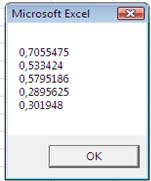
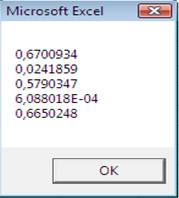
            1 - (300.000-(-100.000))/(500.000-(-100.000)) = 1 – 0,666 = 0,333

A probabilidade será 33%.

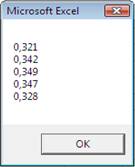
Agora, vamos rodar a simulação e ver o que acontecerá.

Cinco simulações foram rodadas, cada uma com 1000 iterações.  O resultado mostra 5 valores de probabilidades numa caixa de mensagem.  Cada resultado está perto do cálculo matemático de 33%.

Aqui está a sub-rotina que roda uma simulação:

Sub ObterProb()
    Dim alto As Single, baixo As Single, lucro As Single
    Dim contador As Integer
    Dim str As String
   
    alto = 500000
    baixo = -100000
    lucro = 300000
   
    srt = ""
    For j = 1 To 5
       contador = 0
        For i = 1 To 1000
            If lucro <= Rnd * (alto - baixo + 1) + baixo Then
               contador = contador + 1
            End If
        Next i
        str = str & contador / 1000 & vbCrLf
    Next j
   
    MsgBox str
End Sub

Este exemplo é também é implementado no tutorial de Simulação de Monte Carlo tutorial.

(Esta função é semelhante à função ORDEM.PORCENTUAL() fornecida pelo Excel).  

Criando um Histograma

Um histograma de uma simulação mostra a representação gráfica da distribuição de probabilidades derivada. 

O procedimento sub que segue é um modelo melhorado para geração de um histograma.  O primeiro parâmetro, M, é o número de bins (interrupções) que você quer ter no histograma.  O segundo parâmetro é o array que contém aqueles valores para o histograma.

Para este procedimento funcionar adequadamente o array precisa ser ordenado chamando o procedimento histograma.  Desta maneira, os valores máximo e mínimo podem ser derivados e usados para configurar os valores bin.  Por gentileza, veja os exemplos seguintes para a implementação:

Gerador de Número Aleatório com Distribuição Normal, Bootstrap – Uma Abordagem Não Paramétrica,
e Simulação de Monte Carlo.

Aqui estão os códigos que geram um histograma:

Sub Hist(M As Long, arr() As Single)
    Dim i As Long, j As Long
    Dim Comprimento As Single
    ReDim interrupcoes(M) As Single
    ReDim freq(M) As Single
   
    For i = 1 To M
        freq(i) = 0
    Next i

   Comprimento = (arr(UBound(arr)) - arr(1)) / M
   
    For i = 1 To M
       interrupcoes (i) = arr(1) + Length * i
    Next i
   
    For i = 1 To UBound(arr)
        If (arr(i) <= interrupcoes (1)) Then freq(1) = freq(1) + 1
        If (arr(i) >= interrupcoes (M - 1)) Then freq(M) = freq(M) + 1
        For j = 2 To M - 1
            If (arr(i) > interrupcoes (j - 1) And arr(i) <= interrupcoes s(j)) Then freq(j) = freq(j) + 1
        Next j
    Next i
   
    For i = 1 To M
        Cells(i, 1) = interrupcoes (i)
        Cells(i, 2) = freq(i)
    Next i
End Sub

O que segue é um exemplo de resultado do procedimento:

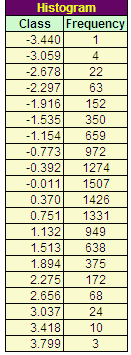
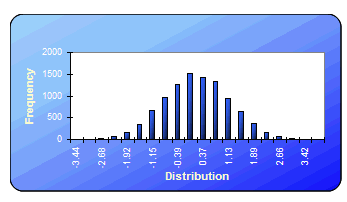
As classes são os bins ou as interrupcoes.  A freqüência contém o número de valores simulados para cada uma das classes.

Aqui está o gráfico do histograma deste exemplo: