Notas de Aula 7

Distribuição Amostral da Média
(Aula Sete)

L.A. Bertolo

Introdução:

Você deve se lembrar da aula um que existem várias boas razões de se tomar uma amostra ao invés de se conduzir um censo, por exemplo, economia de tempo, de dinheiro, etc. Também, na mesma aula dissemos que se um pesquisador usando dados colhidos de um grupo para conseguir conclusões somente sobre aquele mesmo grupo, a estatística é chamada estatística descritiva. Por exemplo, se eu produzir estatística para resumir o esforço no exame da aula e usar esta estatística para obter conclusões sobre minha aula somente, a estatística é descritiva. Por outro lado, se um pesquisador colhe dados de uma amostra e usa a estatística gerada para chegar a conclusões sobre a população da qual a amostra foi retirada, a estatística é estatística inferencial (ou indutiva). Os dados colhidos estão sendo usados para inferir alguma coisa sobre um grupo maior.
Ao se tentar analisar a estatística da amostra, é essencial saber a distribuição da estatística. Nesta aula, iremos falar sobre a média da amostra como a estatística. Para computar e atribuir a probabilidade de ocorrência de um valor particular de uma média amostral, devemos conhecer a distribuição das médias amostrais. Em outras palavras, como as médias amostrais estão distribuídas? Uma maneira de se examinar a distribuição de possibilidades é tomar uma população com uma distribuição particular, selecionar aleatoriamente amostras de ddado tamanho, calcular as médias amostrais, e tentar determinar como as médias estão distribuídas.

Exemplo:

Suponha que numa companhia o fundo de pensão seja investido em cinco ações corporativas com os seguintes retornos:
Ação........................Retorno
A.................................7%
B................................12%
C.................................-3%
D................................21%
E..................................3%

Neste exemplo, a média populacional é igual a 8%, e odesvio padrão da população é igual a 8,15%. Agora, suponha que decidimos pegar uma amostra aleatória de três ações. Assumindo que a ordem não seja importante e a amostragem é feita sem reposição, aplicando a fórmula de combinação (n=5, e x=3) existem dez possibilidades:

Amostra de Ações...............Retornos.............Média

1) A, B, C......................7%..12%..-3%......5,33%
2) A, B, D......................7%..12%..21%....13,33%
3) A, B, E......................7%..12%..3%........7,33%
4) A, C, D......................7%..-3%..21%......8,33%
5) A, C, E......................7%..-3%..3%........2,33%
6) A, D, E......................7%..21%..3%......10,33%
7) B, C, D.....................12%..-3%..21%.....10,00%
8) B, C, E.....................12%..-3%..3%........4,00%
9) B, D, E.....................12%..21%..3%......12,00%
0) C, D, E.....................-3%..21%..3%........7,00%

Como mostra o exemplo acima, duas (ou mais) amostras da mesma população terão provavelmente diferentes valores amostrais (os valores da média variando de 2,33% to 13,33%), e, portanto, possivelmente conduzem a decisões diferentes. Assim, a média amostral reportada tomador de decisões na companhia dependerá da amostra selecionada, i.e., amostra 1, 2, 3,.....ou 10. Note que as médias amostrais (coluna 3 na tabela acima) também são diferentes da média populacional, i.e., 8. Por exemplo, se a amostra 4 for selecionada, o erro amostral (a diferença entre uma estatística amostral e seu correspondente parâmetro populacional) is bastante pequeno (8,33 - 8,0 = 0,33), mas se a amostra selecinada for a amostra 2, o erro é muito grande (13,33 - 8,0 = 5,33). Como o tomador de decisões não pode saber quão grande o erro amostral será anter de selecionar a amostra, ele/ela deverá saber como as possíveis médias amostrais são distribuídas.

Definição:A distribuição de todas as possíveis médias amostrais e suas probabilidades relacionadas é chamada de distribuição amostral das médias.

Propriedades da Distribuição Amostral das Médias:

Se uma população for distribuída normalmente, então:

1. A média da distribuição amostral das médias iguala-se à média populacional.
2. O desvio padrão da distribuição amostral das médias (ou erro padrão das médias) é menor que o desvio padrão da população, veja as seguintes equações

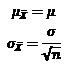
Equação 1

Por exemplo, da tabela acima, a média das médias é igual a 8% que é a mesma que a média populacional, e o erro padrão das médias é igual a 3,26% que é menor que o desvio padrão da população de 8,15%.

Teorema do Limite Central:

Se uma amostra aleatória de n observações for selecionada de qualquer população, então, quando o tamanho da amostra for suficientemente grande (n>=30) a distribuição amostral das médias tende a se aproximar da distribuição normal. Quanto maior o tamanho da amostra, n, melhor será a aproximação normal approximation para a distribuição amostral das médias. Então, novamente neste caso pode ser mostrado que a média das médias amostrais ié a mesma que a média populacional, e o erro padrão das médias é menor que o desvio padrão da população, ver equação 1, acima.

A verdadeira vantagem do teorema do limite central é que a amostra de dados retirada das populações não distribuída normalmente ou de populaçãos de formato desconhecido também pode ser analisada usando a distribuição normal, porque as médias amostrais são distribuídas normalmente para amostras de tamanho n>=30.
A coluna 1 da figura seguinte mostra quatro diferentes distribuições população. Cada coluna seguinte mostra o formato da distribuição das médias amostrais para um particular tamanho de amostra. Note que a distribuição das médias amostrais começa a se aproximar da curva nomal quando a amostra de tamanho, n, ficar maior.

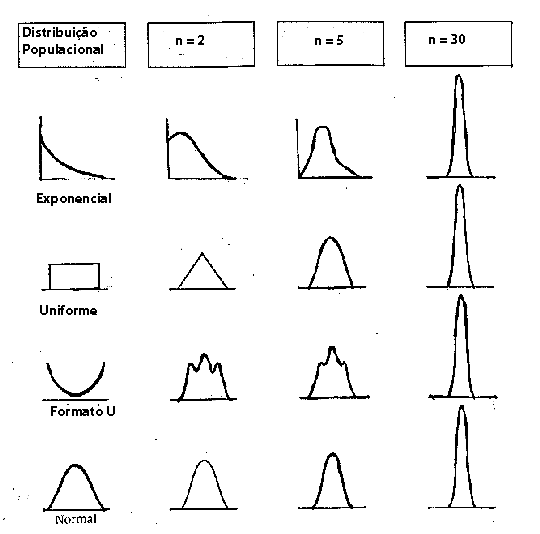
Figura 1

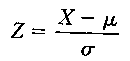
Como o teorema do limite central estabelece que as médias amostrais são distribuída normalmente a despeito do formato da população para amostras grandes e para qualquer tamanho de amostra com uma população distribuída normalmente, então as médias amostrais podem ser analisadas usando Z scores. Lembre-se da aula seis que:

Equação 2

Se as médias amostrais estiverem distribuídas normalmente, a equação Z score aplicada às médias amostrais será:

Equação 3.

Exemplo:

Você é o diretor de segurança dos transportes do estado de Pernambuco. Você está interessado porque a velocidade média nas rodovias todos caminhões podem exceder as 60 km/h como velocidade limite. Uma amostra aleatória de 120 caminhões mostra uma média de velocidade de 62 km/h. Assumindo que a média populacional seja 60 km/h e o desvio padrão da população seja 12,5 km/h, encontre a probabilidade da média das velocidades ser maior que ou igual a 62 km/h.

Neste problema, n= 120, a média das médias = média populacional = 60 km/h, e erro padrão das médias = desvio padrão da população /raiz quadrada do tamanho da amostra = 12,5/10,95 = 1,14. Enfiando estes números na equação Z score (equação 3) obtemos, Z = (62 - 60)/1,14 = 1,75. Da tabela de distribuição normal padronizada, este valor Z leva a uma probabilidade de 0,4599. Esta é a probabilidade de se obter uma média entre 62 km/h e a média populacional 60 km/h. Portanto, a probabilidade de se obter uma velocidade média amostral maior que 62 km/h é (0,5 - 0,4599) = 0,04. Isto é, 4% das vezes, uma amostra aleatória de 120 caminhões da população conduzirão a uma velocidade média de 62 km/h ou mais. A seguinte figura mostra o problema.

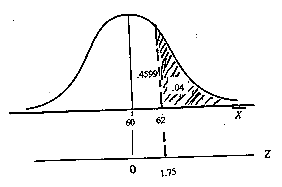
Figura 2

Amostragem de uma População Finita:

Você deve se lembrar da aula seis que uma população finita é uma população que tem um limite limite superior fixo. Por exemplo, há 5.124 estudantes matriculados no IMES Catanduva. No caso de uma população finita, um ajuste é feito na equação Z para as médias amostrais (equação 3 acima). O ajuste é chamado fator de correção, ou multiplicador de população finita.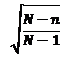

Fator de Correção

Como um princípio é que se a amostragem for feita sem reposição de uma população finita e o tamanho da amostra, n, for maior que 5% do tamanho da população N, i.e., n/N>0,05, então o fator de correção deverá ser usado para ajustar o desvio padrão ( ou erro padrão) das médias. Então, a seguinte equação Z é usada quando amostras forem extraídas de uma população finita.

Equação 4

Exemplo:

A idade média dos 250 empregados horistas do setor de produção de uma companhia é de 39,5 anos, com um desvio padrão de 9,3 anos. Se uma amostra aleatória de 35 empregados horistas for tomada, qual é a probabilidade de que a amostra terá uma idade média menor que 43 anos?
Neste problema, a média populacional é 39,5, com um desvio padrão da população de 9,3. O tamanho da amostra é 35 que é extraída de uma população finita de 250. A média amostral é 43. O gráfico seguinte mostra o problema sobre uma curva normal.

Figura 3

Usando a equação Z com o fator de correção (equação 4 ) dá um Z score de 2,39. Da tabela de distribuição normal padronizada, este valor Z conduz a uma probabilidade de 0,4916. Portanto, a probabilidade de se obter uma média amostral de idades menor que 43 anos é (0,5 + 0,4916) = 0,9916 ou 99,16%. Não tendo usado o fator de correção, o valor Z teria sido 2,23, e a probabilidade de se obter uma idade média amostral menor que 43 anos teria sido 98,71%.

Distribuição Amostral de Proporções Amostrais:

A proporção amostral é calculada dividindo-se o número de itens de uma amostra que possui a característica, X, pelo número de itens da amostra, n.

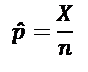
Equação 5

O teorema do limite central também se aplica às proporções amostrais em que a distribuição normal aproxima a forma da distribuição da proporção amostral se (n x p) > 5 e [n (1 - p)] > 5, onde p é a proporção poopulacional.
A média da proporção amostral para todas as amostras de tamanho n extraídas aleatoriamente de uma população é p (a proporção populacional) e o desvio padrão da distribuição amostral das proporções amostrais (ou o erro padrão da proporção) é a raiz quadrada de (p . q)/n, onde q = 1 - p. A equação Z para a proporção amostral é como segue:

Equação 6

Note que equação 6 é usada quando estamos contando itens discretos, tais como pessoas ou defeitos, e estamos interessados em porcentagens ou proporções.
Exemplo:

Suponha que quarenta e três porcento de todas as famílias tinham uma secretária eletrônica em 1994. Maria acredita que esta proporção não pode ser verdadeira para o estado do Piauí. Se ela pegar uma amostra aleatória de 600 famílias e encontrar que somente 135 tem uma secretária eletrônica, qual é a probabilidade de se obter uma proporção amostral que seja pequena ou menor se a proporção populacional realmente for 0,43?

Para este problema, p = 0,43, n = 600, X = 135, e proporção amostral = X/n = 135/600 = 0,23. Usando equação 6, e resolvendo para Z dá Z = (0,23 - 0,43)/raiz quadrada de [(0,43) . (0,57)]/600 = - 10
Quase toda a área sob a curva fica à direita deste valor Z. A probabilidade de obter esta proporção amostral ou uma menor que ela é virtualmente zero. Isto é, o resultado obtido desta amostra são bem diferentes da proporção 43% para Maria aceitar um quadro nacional para o estado do Piauí. O gráfico seguinte mostra este problema.

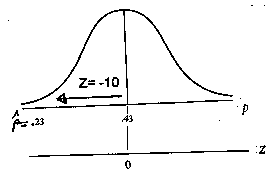
Figura 4

Links relacionados a esta aula