Distribuição Contínua de Probabilidade
(Aula Seis)
![]()
Distribuição Contínua de Probabilidade
(Aula Seis)
![]()
 |
Luiz A. Bertolo
Introdução:
Na aula número quatro dissemos que uma variável aleatória contínua é uma variável que pode tomar qualquer valor num dado intervalo. As variáveis contínuas são medidas, não contadas.
Itens tais como altura, peso e tempo são contínuas e podem tomar valores decimais. Por
exemplo, um jogador de basketball pode ter 2,10 m de altura.
Existem muitas distribuições de probabilidades contínuas, tais como, distribuição uniforme, distribuição normal, a distribuição t, a distribuição chi-quadrado, distribuição exponencial, e distribuição F. Nesta nota de aula, concentrar-nos-emos na distribuição uniforme, e distribuição normal.
Distribuição Uniforme (ou Retangular):
Entre as distribuições de probabilidades contínuas, a distribuição uniforme é a mais simples de todas. A figura seguinte mostra um exemplo de uma distribuição uniforme. Numa distribuição uniforme, a área sob a curva é igual ao produto do comprimento pela altura do retangulo e igual a 1.

Figura 1
onde: a=limite inferior do intervalo, e b= limite superior do intervalo.
Note que no gráfico acima, como a área do retângulo = (comprimento)(altura) =1, e como o comprimento = (b - a), então podemos escrever: (b - a)(altura) = 1 ou altura = f(X) = 1/(b - a).
As equações seguintes são usadas para se encontrar a média e o desvio padrão de uma distribuição uniforme:

Exemplo:
Existem muitos cassos nos quais podemos ser capazes de aplicar a distribuição uniforme. Como um exemplo, suponhamos que o departamento de pesquisa de uma fábrica de aço acredita que uma das máquinas de rotação da companhia esteja produzindo folhas de aço de diferentes espessuras. A espessura é uma variável aleatória uniforme com os valores entre 150 e 200 milímetros. Qualquer folha com menos de 160 milímetros de espessura deve ser descartada devido serem inaceitáveis pelos compradores. Queremos calcular a média e o desvio padrão de X (a espessura da folha produzida por esta máquina), e a fração das folhas de aço produzidas por esta máquina que terão de ser descartadas. A figura seguinte mostra a distribuição uniforme para este exemplo.

Figura 2
Note que para distribuições contínuas, a probabilidade é calculada encontrando-se a área sob a função num determinado intervalo específico. Em outras palavras, para distribuições contínuas, não há probabilidade em um dado ponto. A probabilidade de X>= b ou de X<= a é zero porque não há área acima de b ou abaixo de a, e a área entre a e b é igual a 1, ver figura 1.
A probabilidade das variáveis caírem entre quaisquer dois pontos, tal como c e d na figura 2, são calculadas como segue:
P (c <= x <=d) = c*[1/(b - a)] = ?
Neste exemplo c=a=150, d=160, e b=200, portanto:
Média = (a + b)/2 = (150 + 200)/2 = 175 milímetros.
O desvio padrão é igual a 14,43 milímetros, e P(c <= x <=d) = [(160-150)/(200-150)] = "1/5" assim, de todas as folhas feitas por esta máquina, 20% da produção deve ser descartada).
Distribuição Normal ou Curva Normal
Distribuição normal é provavelmente uma das mais importantes e largamente usadas das distribuições contínuas. Ela é conhecida como uma variável aleatória normal, e sua distribuição de probabilidade é chamada de distribuição normal. O que segue são características da distribuição normal:
Características da Distribuição Normal:
1. Ela tem a forma de um sino e é simétrica ao redor da sua média.
2. Ela se aproxima assintoticamente do eixo, i.e., ela se estende indefinidamente em qualquer direção a partir da média.
3. Ela é uma distribuição contínua.
4. Ela é uma familia de curvas, i.e., cada par único de média e desvio padrão define uma distribuição normal diferente. Assim, a distribuição normal é completamente descrita por dois parâmetros: média e desvio padrão. Ver a seguinte figura.
5. A área total sob a curva totaliza 1, i.e., a área da distribuição em cada lado da média é 0,5.
6. Ela é unimodal, i.e., os valores acumulam-se somente no centro da curva.
7. A probabilidade que uma variável aleatória terá um valor eentre dois pontos quaisquer é igual à área sob a curva entre aqueles pontos.
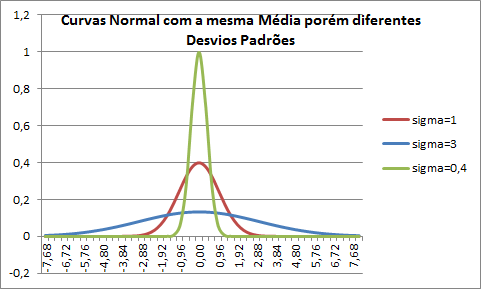 |
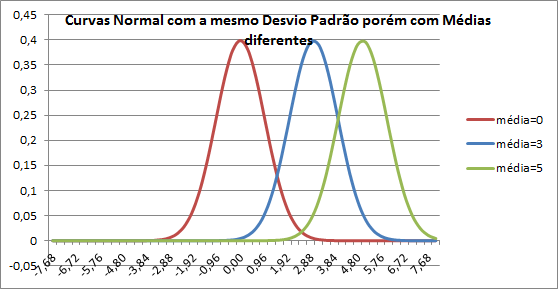 |
|---|
Figura 3
Para construir um gráfico da curva normal no Excel basta clicar aqui.
Note que o cálculo integral é usado para encontrar a área sob a curva de distribuição normal. Entretanto, isto pode ser evitado transformando toda distribuição normal para ajustar-se à distribuição normal padrão. Esta conversão é feita rescalonando o eixo da distribuição normal de suas unidades verdadeiras (tempo, peso, dólares, e...) para uma medida padrão chamada Z score ou Z value. Um Z score é o número de desvios padrões que um valor, X, está fora da média. Se o valor de X for maior que a média, o Z score é positivo; se o valor de X for menor que a média, o Z score é negativo. A equação do Z score é como segue:
Z = (X - Média) /Desvio padrão
Uma tabela do Z padronizado pode ser usada para encontrar as probabilidades para qualquer problema de curva normal que tenha sido convertido para Z scores. Para a tabela, refira-se ao texto. A distribuição Z é uma distribuição normal com média 0 e desvio padrão 1.
Os passos seguintes são úteis quando se trabalha com problemas de curva normal:
1. Gráfico da distribuição normal, e a área sombreada estão relacionados à probabilidade que você quer encontrar.
2. Converter os limites da área sombreada dos valores de X para os valores da variável aleatória normal padronizada Z usando a fórmula de Z acima.
3. Usar a tabela Z padrão para encontrar as probabilidades ou as áreas relacionadas aos valores de Z do passo 2.
4. Se você preferir, pode realizar os cálculos usando uma página em javascript para a distribuição normal.
Exemplo Um:
Os escores do Graduate Management Aptitude Test (GMAT) são largamente usados pelas escolas de pós graduação de negócios como uma exigência de matrícula. Suponha que num dado ano particular, o escore médio para o GMAT foi 476, com um desvio padrão de 107. Assumindo que os escores GMAT estão normalmente distribuídos, responda as questões seguintes:
Questão 1. Qual é a probabilidade que um escore selecionado aleatoriamente deste GMAT caia entre 476 e 650? <= x <="650)" a figura seguinte mostra uma representação gráfica deste problema.

Figura 4
Aplicando a equação , obtemos: Z = (650 - 480)/107 = 1,58. O valor Z de 1,58 indica que o GMAT score de 650 está 1,58 desvios padrão acima da média.
A tabela normal padrão dá a probabilidade do valor cair entre 650 e a média.
O número completo e a porção das casas decimais do Z score aparecem na primeira coluna da tabela normal padronizada. Pelo topo da tabela são os valores da porção centesimal do Z score. Assim a resposta é que 0,4452 ou 44,52% dos scores no GMAT caíram entre um score de 650 e 480.
Questão 2. Qual é a probabilidade de se receber um escore maior que 750 num teste GMAT que tenha média de 480 e um desvio padrão de 107?
i.e., P(X >= 750) = ?. Este problema é respondido determinando-se a área da cauda superior da distribuição. O Z score é: Z = ( 750 - 480)/107 = 2,52. Da tabela, a probabilidade para este Z score é 0,4941. Esta é a probabilidade de um GMAT com um escore entre 480 e 750. A regra é que quando queremos encontrar a probabilidade numa cauda, devemos subtrair o valor da tabela de 0,50. Assim, a resposta para este problema, usando a tabela normal é: 0,5 - 0,4941 = 0,0059 ou 0,59%. Note que P(X >= 750) é o mesmo que P(X >750), porque, com distribuição contínua, a área sob um número exato tal como X=750 é zero. A figura seguinte mostra uma representação gráfica deste problema.

Figura 5
Questão 3. Qual é a probabilidade de se receber um score de 540 ou menos num teste GMAT que tenha uma média 480 e um desvio padrão de 107?, i.e., P(X <= 540)="?". Estamos perguntando para se determinar a área sob a curva para todos valores menores ou iguais a 540. O z score é: z=(540 - 480)/107="0,56". Da tabela, a probabilidade para este z score é 0,21226 que é a probabilidade de se obter um escore entre a média (476) e 540. A regra é que quando queremos encontrar a probabilidade entre dois valores de x num lado da média, apenas adicionamos as duas área juntas. Assim, a resposta para este problema é 0,5 + 0,21226 = 0,7123 ou 71,25%. A figura seguinte mostra uma representação gráfica deste problema.

Figura 6
Questão 4. Qual é a probabilidade de se receber um score entre 440 e 330 num teste GMAT que tenha uma média de 480 e um desvio padrão de 107?, i.e., P(330<X< 440)="?". A solução para este problema envolve a determinação da área da porção hachuriada na metade inferior da curva na figura seguinte.
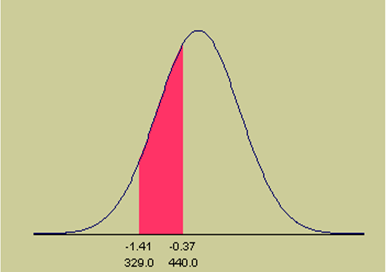
Figura 7
Neste problema, os dois valores caem do mesmo lado da média. Os Z scores são: Z1 = (330 - 480)/107 = -1,4019, e Z2 = (440 - 480)/107 = -0,3738. Assim, usando a tabela normal,
0,422196 - 0,144309 = 0,2779 ou 27,79%.
Exemplo Dois:
Suponha que uma fábrica de pneus queira montar uma garantia de quilometragem do seu novo modelo chamado LA 50. Teste de vida indicaram que a quilometragem média é 47.900, e desvio padrão da distribuição normalmente distribuída da quilometragem é de 2.050 quilômetros. A fábrica quer montar a garantia de quilometragem de modo que não mais do que 5% dos pneus terão de ser substituídos. Qual a garantia de quilometragem deveria a fábrica anunciar? i.e., P(X <= ?)="5%". Neste problema, a média e o desvio padrão são dados, mas X e Z são desconhecidos. O problema é encontrar um valor de X que tenha 5% ou 0,05 dos valores de X menores do que aquele valor. Se 0,05 dos valores são menores que X, então 0,45 ficam entre X e a média (0.5 - 0,05), veja o gráfico seguinte:
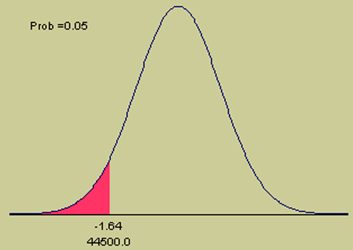
Figura 8
Recorra à tabela de distribuição normal padronizada e procure no corpo da tabela por 0,45.
Como o número exato não é encontrado na tabela, procure por aquele número mais próximo a 0,45.
Existem dois valores equidistantes de 0,45-- 0,4505 e 0,4495. Mova-se para a esquerda destes valores, e leia os Z scores na margem, que são: 1,65 e 1,64. Tome a média destes dois Z scores, i.e., (1,65 + 1,64)/2 = 1,645. Coloque este número e os valores da média e do desvio padrão na equação Z, você obtém:
Z =(X - média)/desvio padrão ou -1,645 =(X - 47.900)/2.050 = 44.528 milhas.
Assim, a fabrica deverá montar a quilometragem de garantia em 44.528 quilômetros se o objetivo não for trocar mais que 5% dos pneus.
A Aproximação Normal para a Distribuição Binomial:
Na nota de aula número 5 falamos acerca da distribuição binomial de probabilidades, que é uma distribuição discreta. Você se lembra que dissemos que quando o tamanho das amostras ficam maiores, a distribuição binomial aproxima-se da distribuição normal na forma a despeito do valor de p (probabilidade de successo). Para valores de amostra grande, a distribuição binomial é enfadonha de ser analisada sem um computador. Felizmente, a distribuição normal é uma boa aproximação para os problemas de distribuição binomial para valores de n grandes. A orientação comumente aceita para se usar a aproximação normal para a distribuição binomial de probabilidades é quando (n x p) e [n(1 - p)] forem ambos maiores que 5.
Exemplo:
Suponha que o gerente de um restaurante reivindicasse que 70% dos seus clieentes retornassem para outra refeição. Numa semana em que 80 novos (primeira vez) clientes jantaram no restaurante, qual é a probabilidade que 60 ou mais dos clientes retornarão para uma outra refeição?, ie., P(X >= 60) =?.
A solução para este problema pode ser ilustrada como segue:
Primeiro, as duas orientações que (n x p) e [n(1 - p)] deverão ser maior que 5 são satisfeitas: (n x p) = (80 x 0,70) = 56 > 5, e [n(1 - p)] = 80(1 - 0.70) = 24 > 5.
Segundo, precisamos encontrar a média e o desvio padrão da distribuição binomial.
A média é igual a (n x p) = (80 x 0,70) = 56 e o desvio padrão é a raiz quadrada de [(n x p)(1 - p)], i.e., raiz quadrada de 16,8, que ée igual a 4,0988. Usando a equação Z obtemos, Z = (X - média)/desvio padrão = (59,5 - 56)/4,0988 = 0,854. Da tabela, a probabilidade para este Z score é 0,302338 que é a probabilidade entre a média (56) e 60. Devemos subtrair este valor da tabela 0,302338 de 0,5 para obter a resposta, i.e., P(X >= 60) = 0,5 -0,302338 = 0,1977. Portanto, a probabilidade é 19,77% que 60 ou mais dos 80 clientes pela primeira vez retornarão ao restaurante para outra refeição. Veja o gráfico seguinte.
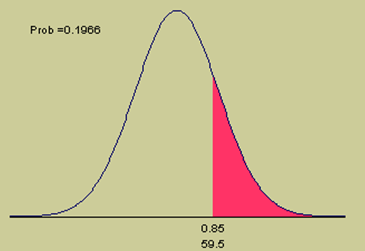
Figura 9
Fator de Correção:
O valor 0,5 é adicionado ou subtraído, dependendo do problema, ao valor de X quando uma distribuição binomial de probabilidades estiver sendo aproximada por uma distribuição normal. Esta correção assegura que a maioria das informações dos problemas binomial é transferida corretamente para a análise da curva normal. Esta correção é chamada de correção para a continuidade. A decisão de como corrigir pela continuidade depende do sinal de igualdade e da direção dos resultados desejados da distribuição binomial. A seguinte tabela mostra alguns princípios básicos que podem ajudar na aplicação da correção para a continuidade, ver exemplo acima.
Valor Sendo Determinado..............................Correção
X >..................+0,50
X > =...............-0,50
X <..................-0,50
X <=...............+0,0
<= X <="...................................-0,50" & +0.50
<........................................+0,50 & 0,50<........................................+0,50 & 0,50<........................................+0,50 & 0,50<........................................+0,50 & 0,50<........................................+0,50 & 0,50<........................................+0,50 & 0,50<........................................+0,50 & 0,50<........................................+0,50 & 0,50<........................................+0,50 & 0,50<........................................+0,50 & 0,50<........................................+0,50 & 0,50<........................................+0,50 & 0,50
X =.............................................-0,50 & +0,50
Links
relacionados à esta aula
![]()
All contents copyright (c) 2012.
All rights reserved.
Esta página
foi alterada pela última vez em
14/7/12