Notas de Aula 3

Estatística Descritiva
(Aula Três)

L.A. Bertolo

Introdução:

O propósito desta aula é ajudá-lo a entender conceitualmente o significado das medidas de posição (i.e., média, mediana e moda) e medidas de dispersão (i.e., amplitude, variância, desvio padrão e coeficiente de variação).

Medidas de Posição para Dados Brutos ou Não Agrupados:

Medidas de posição dá informações sobre localização num grupo de números ou dados. As medidas de posição apresentadas nesta nota de aula para dados não agrupados (brutos) são a média, a medianaa, e a moda.

Média Aritmética:

A média aritmética (ou simplesmente média) é calculada somando-se todos os números e dividindo-se pelo número de observações. Por exemplo, para calcular a média aritmética de uma amostra de números, tais como 19, 20, 21, 23, 18, 25, e 26, primeiro some os números: (19+20+21+23+18+25+26) = 152, e daí então calcule a média da amostra dividindo-se este total (152) pelo número de observações (7), que dá uma média de 21,7 ou cerca de 22.
A média usa todas as observações e cada observação afeta a média. Muito embora a média seja sensível aos valores extremos (i.e., dados extremamente grandes ou pequenos podem fazer com que a média seja puxada para os dados extremos) ela é ainda a medida de posição mais largamente usada. Isto é devido ao fato de que a média tem propriedades matemáticas valiosas que a torna conveniente para se usar com análise estatística inferencial. Por exemplo, a soma dos desvios dos números de um conjunto de dados da média é zero, e a soma dos desvios quadrados dos números de um conjunto de dados da média é o valor mínimo. Estes pontos serão explicados em detalhes na aula número 14.

Média Ponderada:

Em alguns casos os dados na amostra ou população não deverão ser igualmente ponderados, e cada valor é ponderado de acordo com sua importância. Por exemplo, suponha que Alessandro queira encontrar sua média num curso de estatística, e assuma que os exames são ponderados como segue:

Primeiro Teste...............100 Pontos...............15%
Segundo Teste..............100 Pontos...............20%
Terceiro Teste...............100 Pontos...............25%
Teste Final.....................100 Pontos...............30%
Trabalhos.......................050 Pontos...............10%
Pontos Disponíveis.......450 Pontos...............100%

Assuma que Alessandro conseguiu 90, 71, 87, 77, e 40 no primeiro teste, segundo teste, terceiro teste, exame final, e os trabalhos, respectivamente. A média de Alessandroe no curso de estatística é como segue:
(90x0,15+71x0,20+87x0,25+77x0,30+40x0,10)/(0,15+0,20+0,25+0,30+,010)=76,55 ou 77 pontos.

Mediana

A mediana é o valor do meio num arranjo ordenado de observações. Se existe um número par de dados no arranjo, a mediana é a média dos dois números centrais. Se houver um número ímpar de dados no arranjo, a mediana é o número central. Por exemplo, suponha que você queira encontrar a mediana para o seguinte conjunto de dados:

74, 66, 69, 68,73, 70

Primeiro, arrumemos os dados num arranjo ordenado (ROL):

66, 68, 69, 73, 70, 74

Desde que há um número par de dados, a média dos dois números centrais(i.e., 69 e 73) é a mediana (142/2 = 71). Note que em geral, aposição da mediana é=(n+1)/2 onde n=número total de itens.

Geralmente, a mediana fornece uma medida de posição melhor do que a média quando existem algumas observações extremamente grandes ou pequenas (i.e., quando os dados são distorcidos parra a direita ou para a esquerda). Por esta razão, a renda mediana é usada como a medida de posição para a renda familiar nos U.S.A. Note que se a mediana for menor do que a média, o conjunto de dados é distorcido para a direita (i.e., os dados tendo limites inferiores mas não limites superiores resultarão numa distorção positiva para a direita). Se a mediana for maior que a média, o conjunto de dados é distorcido para a esquerda (os dados têm limite superior mas não têm limite inferior resultarão numa distorção negativamente para a esquerda). A mediana não tem propriedades matemáticas importantes para uso nos cálculos futuros. Ver a figura seguinte:

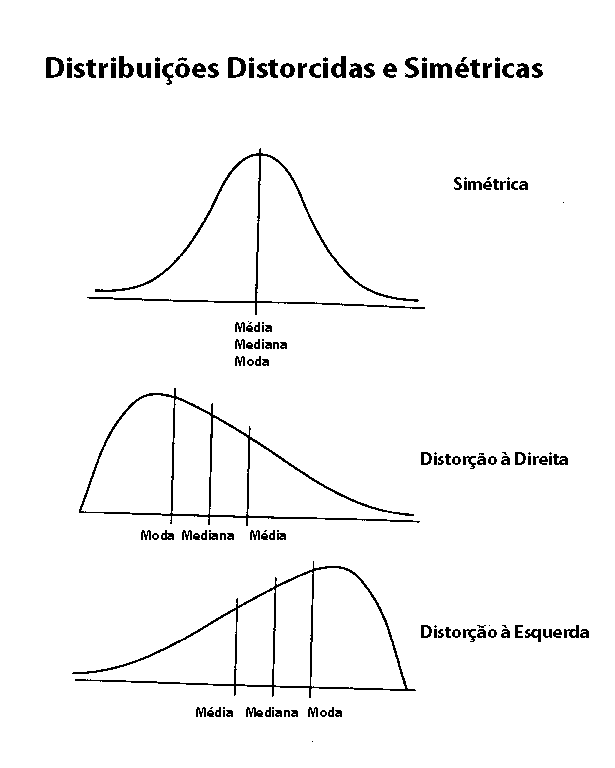
Moda:

A moda é o valor que ocorre mais frequentemente num conjunto de observação. Por exemplo, dado 2, 3, 4, 5, 4, a moda é 4, porque existem mais quatro do que qualquer outro other número. Os dados podem ter duas modas. Neste caso podemos dizer que os dados são bimodal, e observações com mais do que duas modas são refernciadas como multimodal. Note que a moda não tem propriedades matemáticas importantes para uso futuro. Também, a moda não é uma medida de posição útil, porque podem existir mais do que uma moda ou mesmo nenhuma moda.

Medidas de Variabilidade para Dados Brutos ou Não Agrupados:

Medidas de variabilidade representam a dispersão de um conjunto de dados. Por exemplo, voltemos aos graus de Alessandro no curso de estatística:
Alessandro conseguiu 90, 71, 87, 77, e 40 no primeiro teste, segundo teste, terceiro teste, exame final e nos trabalhos, respectivamente. Lembre-se que a média de Alessandro no curso foi 77. O que significa este score médio para Alessandro? Ele deverá estar satisfeito com esta informação? Medidas de posição (média neste caso) não produz informação grande o suficiente ou adequada para descrever o conjunto de dados. O que é necessário é uma medida de variabilidade dos dados. Note que um pequeno valor para uma medida de dispersão indica que os dados estão ao redor da média; portanto, a média é uma boa representação do conjunto de dados. Por outro lado, uma grande medida de dispersão indica que a média não é uma boa representação do conjunto de dados. Também, medidas de dispersão podem ser usadas quando quisermos comparar as distribuições de dois ou mais conjuntos de dados. Nesta aula falaremos sobre amplitude, variância, desvio padrão, e coeficiente de variação para dados não agrupados ou brutos.

Amplitude:

A amplitude é a diferença entre a maiorv observação de um conjunto de dados e a menor observação. A maior desvantagem da amplitude é que ela não inclui todas as observações. Somente os dois valores mais extremos são incluídos e estes dois números podem ser observações atípicas. Por exemplo, dado que as idades para uma amostra de 8 estudantes no CSC são: 24, 18, 22, 19, 25, 20, 23, e 21, a amplitude para este conjunto de dados é: 25 - 18 = 7.

Variância:

Uma importante medida de variabilidade é a variância. Variância é a média dos desvios quadrados da média aritmética. Por exemplo, suponha que o peso(em kg) de uma amostra de estudantes no IMES são como segue:

Peso em kg
66
73
68
69
74

Os passos seguintes são usados para calcular a variância:

1. Encontre a média aritmética.
2. Encontre a diferença entre cadavobservação e a média.
3. Eleve ao quadrado estas diferenças.
4. Some as diferenças ao quadrado.
5. Como os dados são de uma amostra, divida o número (do passo 4 acima) pelo número de observações menos um, i.e., n-1 (onde n é igual ao número de observações no conjunto de dados). Posteriormente, este termo (n-1) será chamado de graus de liberdade.

Seguindo os passos acima, a variância é como segue:

Peso..................Desvios..............Desvios
(Kg).............................................Quadrados

66.......................66-70= - 4.............16
73.......................73-70= +3..............09
68.......................68-70= - 2..............04
69.......................69-70= - 1..............01
74.......................74-70= +4..............16

Total da coluna um = 350, e total da coluna três = 46
Média aritmética = (350)/(5) = 70 kg e variância = (46)/(5-1) = 11,5 kg ao quadrado.

Como você viu no exemplo acima, a variância não é expressa nas mesmas unidades que as observações. Em outras palavras, a variância é difícil para se entender porque os desvios da média estão ao quadrado, tornando-o muito grande para explicações lógicas. Estes problemas podem ser resolvidos trabalhando com a raiz quadrada da variância, que é chamada desvio padrão.

Desvio Padrão:

Ambas variância e o desvio padrão fornecem as mesmas informações; pode-se sempre ser obtido um do outro. Em outras palavras, o processo de se calcular um desvio padrão sempre envolve calcular a variância. Como dissemos, desde que o desvio padrão é a raiz quadrada da variância, ele é sempre expresso na mesmas unidades que os dados brutos. Por exemplo, no problema acima a variância era 11,5 kg quadrados. O desvio padrão é a raiz quadrada de 11,5 que é igual a 3,4 kg (expresso nas mesmas unidades que os dados brutos).

Significado do Desvio Padrão:

Uma maneira de explicar o desvio padrão como uma medida de variação de um conjunto de dados é responder questões tais como quantas medidas estão dentro de um , dois, e três desvios padrões da média. Para responder questões tais como esta, precisamos falar sobre a regra empírica e regra de Chebyshev. As regras seguintes apresentam as orientações para ajudar a responder as questões de quantas medidas caem dentro de 1, 2, e 3 desvios padrões.

Regra Empírica:

Esta regra geralmente se aplica a dado na forma de monte, mais especificamente aos dados que são normalmente distribuídos, i.e., forma de sino. A regra é como segue:

Aproximaddamente 68% das medidas (dados) cairão dentro de um desvio padrão da média, 95% cairão dentro de dois desvios padrões, e 97,7% (ou quase 100% ) ficam dentro de três desvios padrões. Ver a figura seguinte:

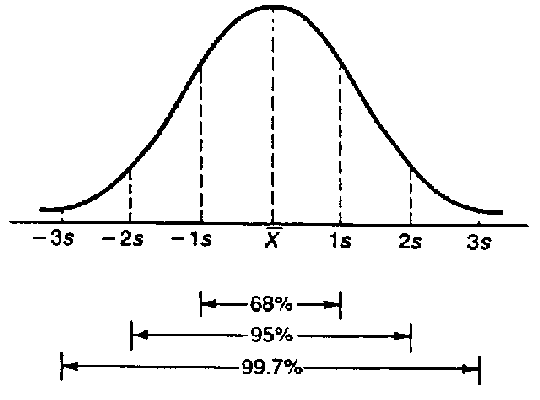
Por exemplo, no problema dos pesos, o peso médio foi 70 kg com um desvio padrão de 3,4 kg. Então, 68% dos pesos ficam entre 66,6 e 73,4 kg, um desvio padrão, i.e., (média + 1 desvio padrão) = (70 + 3,4) = 73,4, e (média - 1 desvio padrão) = 66,6. Noventa e cinco porcento (95%) dos pesos ficam entre 63,2 e 76,8 kg, dois desvios padrões. Noventa e nove e sete décimos de porcentagem (99.7%) ficam entre 59,8 e 80,2 kg, três desvios padrões. Veja a figura seguinte:

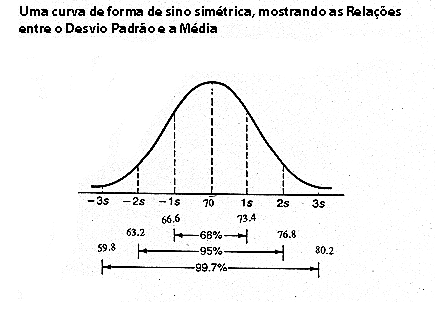
Z Score:

Podemos pegar qualquer ponto no eixo X da figura acima e descobrir quantos desvios padrões acima ou abaixo da média aquele ponto se encontra. Em outras palavras, um Z score representa o número de desvios padrões uma observação (X) está acima ou abaixo da média. Quanto maior o Z valor, mais distante o valor estará da média. Note que valores além de três desvios padrões são muito improváveis. Note que se um Z score for negativo, a observação (X) está abaixo da média. O Z score é encontrado usando a seguinte relação:

Z = (um dado valor - média) / desvio padrão

Por exemplo, para um conjunto de dados que está normalmente distribuídos com uma média de 25 e um desvio padrão de 5, você quer encontrar o Z score para um valor de 35. Este valor (X = 35) está 10 unidades acima da média, com um Z valor de:

Z = (35 - 25)/(5) = (10)/(5) = +2

Estes Z score mostram que os scores brutos (35) estão dois desvios padrões acima da média. Seria plausível obter um grau neste curso que esteja 2 desvios padrões acima da média da classe? O tópico de Z score será discutido em mais detalhes na nota de aula seis.

Regra de Chebyshev:

A regra de Chebyshev se aplica a qualquer amostra de medidas a despeito da forma de sua distribuição. A regra estabelece que:

É possível que nenhuma das medidas caiam dentro de um desvio padrão da média. No mínimo 75% (ou 3/4) das medidas cairão dentro de dois desvios padrões da média, e 89% (ou 8/9) das medidas cairão dentro de três desvios padrões da média.
Geralmente, de acordo com esta regra, no mínimo 1 - (1/k quadrado) das medidas cairão dentro [(média + - (k) desvio padrão)], i.e., dentro k desvio padrão da média, onde k é qualquer número maior que um. Por exemplo, se k = 2,8, no mínimo 0,87 dos valores cairão dentro (média + - 2,8 x desvios padrões), porque 1 - (1/k squared) = 1 - (1/7,84) = 1 - 0,13 = 0,87.

Coeficiente de Variação:

Dissemos que o desvio padrão mede a variação num conjunto de dados. Para distribuições tendo a mesma média, a distribuição com o maior desvio padrão tem a maior variação. Mas quando se considera distribuições com diferentes médias, os tomadores de decisão não podem comparar a incerteza na distribuição somente comparando os desvios padrões. Neste caso, o coeficiente de variação é usado, i.e., os coeficientes de variação para diferentes distribuições são comparados, e a distribuição com o maior valor do coeficiente de variação tem a maior variação relativa.

O coeficiente de variação expressa o desvio padrão como uma porcentagem da média, i.e., ela reflete a variação numa distribuição relativa à média:

Coeficiente de Variação (C.V.) = (desvio padrão / média) x 100

Por exemplo, Marcos ensina estatística em dois períodos. Ele dá para cada período um teste diferente cobrindo o mesmo material. O score médio no teste para o período é 27, com um desvio padrão de 3,4. O escore médio para o período noturno é 74 com um desvio padrão de 8,0. Qual o período tem maior variação ou dispersão dos scores?

Período Diurno....................Período Noturno

Média.......27.......................94
Desv Pad............03,4..................08,0

Comparação direta dos dois desvios padrões mostram que o período noturno tem uma variação maior. Mas comparando os coeficientes de variações mostram resultados bem diferentes:

C.V.(diurno) = (3,4/27) x 100 = 12,6% e C.V.(noturno) = (8/94) x 100 = 8,5%

Assim, baseado no tamanho do coeficiente de variação, Marcos acha que o teste do período noturno resultou uma menor variação relativa à média do que o teste do período diurno.

Links relacionados a esta aula