Organizando & Apresentando Dados
(Aula Dois)
![]()
Organizando & Apresentando Dados
(Aula Dois)
![]()
 |
L.A. Bertolo
Introdução:
O problema que a maioria dos tomadores de decisões devem resolver é como tratar com a incerteza que é inerente em quase todos os aspectos de seus trabalhos. Dados brutos fornece pouca, se alguma, informação aos tomadores de decisão. Então, eles precisam de um mmeio de conversão dos dados brutos numa informação útil. Nesta nota de aula, concentraremos em alguns dos métodos frequentemente usados para apresentar e organizar os dados.
Distribuição de Frequências:
O método mais fácil de se organizar dados é uma distribuição de frequência, que converte os dados brutos numa configuração útil para análises estatísticas.
A seguir estão os passos de construção de uma distribuição de frequências:
1. Especificar o número de intervalos de classe. Uma classe é um grupo (categoria) de interesse. Nenhuma regra totalmente aceita nos diz quantos intervalos devem ser usados. Entre 5 e 15 intervalos de classe são geralmente recomendados. Note que as classes devem ser mutuamente excludentes e totalmente inclusivas. Mutuamente excludentes significa que as classes devem ser selecionadas tais que um item não possa cair em duas classes, e classes totalmente inclusivas são classes que juntas contém todos os dados.
2. Quando todos os intervalos tiverem a mesma largura, a sefguinte regra deve ser usada para se encontrar a largura exigida do intervalo de classe:
W = (L - S) / K
onde:
W= largura da classe, L= o maior dado, S= o menor dado, K= número de classes
Exemplo:
Suponha que a idade de uma amostra de 10 estudantes sejam:
20,9, 18,1, 18,5, 21,3, 19,4, 25,3, 22,0, 23,1, 23,9, e 22,5
Selecionamos K=4 e W=(25,3 - 18,1)/4 = 1,8 que é arredondado para 2. A tabela de frequência é como segue:
Intervalo de Classe...............Classe
Frequência............Frequência Relativa
18-U-20...................................................3................................................30%
20-U-22...................................................2................................................20%
22-U-24...................................................4................................................40%
24-U-26...................................................1................................................10%
Note que a soma de todas as frequências relativas deve sempre ser iguais a 1,00 ou 100%. No exemplo acima, vemos que 40% de todos os estudantes são mais novos que 24 anos, porém mais velhos que 22 anos. Frequência relativa
pode ser determinada para dados quantitativos e qualitativos e é uma base conveniente para comparação de grupos similares de tamanhos diferentes.
O Que a Distribuição de Frequência Nos Diz:
1. Ela mostra como os grupos de observações rodeiam um valor central; e
2. Ela mostra o grau das diferenças entre observações.
Por exemplo, no problema acima sabemos que nenhum estudante é mais novo que 18 e a idade abaixo de 24 é mais típica. A idade mais comum está entre 22 e 24, que da informação geral sabemos ser superior àquela usual para os estudantes que entram na faculdade logo após o ensino médio e se graduam por volta de 22 anos de idade. Os estudantes na amostra são geralmente mais velhos. É possível que a população seja constituída de estudantes noturnos que buscam seus títulos numa parte do tempo enquanto mantém o trabalho em tempo integral. Esta análise descritiva fornece-nos uma imagem de amostra de estudantes, que não está disponível nos dados brutos. Como veremos na aula número 3, a distribuição de frequências é a base para a teoria de probabilidades.
Limites de Classes Verdadeiros & Estabelecidos:
Classes Verdadeiras são aquelas classes tais que o limite superior verdadeiro (ou real) de uma classe é o mesmo que o limite inferior da próxima classe.
Por comparação, os limites de classe estabelecidos e limites de classe verdadeiros (real) são dados na tabela seguinte:
Limite Estabelecido................Limite Verdadeiro
$600 - $799.......................................$599.50 até mas não incluindo $799,50
$800 - $999.......................................$799.50 até mas não incluindo $999,50
Na primeira coluna da tabela acima os dados foram arredondados ao dólar mais próximo. Por exemplo, $799,50 foi arredondado para $800 e
contado na segunda classe. Qualquer quantia acima de $799 mas abaixo de $799,50 foi arredondado para $799 e incluído na primeira classe. Então, a classe $600 - $799 realmente inclui todos os dados de $599,50 inclusive até mas não incluindo $799,50.
Distribuição de Frequências Acumuladas:
Quando as observações são numéricas, a frequência acumulada é usada. Ela mostra o número total de observações que ficam acima ou abaixo de certos valores chaves.
Frequência Acumulada para uma população = frequência de cada intervalo de classe + frequências dos intervalos precedentes. Por exemplo, a frequência acumulada para o problema acima é: 3, 5,
9, e 10.
Apresentação dos Dados:
Gráficos, curvas e diagramas são usados para apresentar dados. Diagrama de Barras são usados para graficar dados qualitativos. As barras que não se tocam, indicando que os atributos são categorias qualitativas, variáveis são discretas e não contínuas.
Histogramas são usados para graficarem frequências acumuladas, relativas e absolutas.
Ogiva é também usada para graficar a frequência acumulada. Uma ogiva é construída colocando um ponto correspondente ao extremo superior de cada classe numa altura igual à frequência acumulada da classe. Estes pontos são então ligados. Uma ogiva mostra também a distribuição de frequências acumulada relativa no eixo do lado direito.
Um menos a ogiva mostra quantos itens na distribuição tem um valor menor que o limite superior de cada classe.
Um mais a ogiva mostra quantos itens na distribuição tem um valor superior ou igual ao limite inferior de cada classe.
Um menos o polígono da frequência acumulada é constuído usando os limites superiores verdadeiros e as frequências acumuladas.
Um mais o polígono da frequência acumulada é construído usando os limites inferiores verdadeiros e as frequências acumuladas.
Gráfico de Pizza é frequentemente usado em jornais e revistas para descrever orçamentos e outras informações econômicas. Um ciclo completo (a pizza) representa o número total de medidas. O tamanho de uma fatia é proporcional à frequência relativa de uma categoria particular. Por exemplo, como um ciclo completo é igual a 360 graus, se a frequência relativa para uma categoria for 0,40, o pedaço atribuído àquela categoria é 40% de 360 ou (0,40)(360)= 144 graus.
Gráfico de Pareto é um caso especial do diagrama de barras e usado frequentemente em controle de qualidade. O propósito deste diagrama é mostrar as causas principais da qualidade inaceitável. Cada barra no diagrama mostra o grau do problema de qualidade para cada variável medida.
Gráfico de Séries Temporais é um gráfico em que o eixo X mostra os períodos de tempo e o eixo Y mostra os valores relacionados à estes períodos de tempo.
Gráfico de Ramos e Folhas oferecem um outro método para organizar dados brutos em grupos.
Estes tipos de gráficos são semelhantes ao histograma exceto que os dados reais são mostrados ao invés de barras. O ramo e folhas é desenvolvido primeiro determinando os ramos e depois adicionando as folhas. Os ramos contém os dígitos de valores mais altos e as folhas contém os dígitos de valores mais baixos. Por exemplo, o número 78 pode ser representado por um ramo de 7 e uma folha de 8. Então, os números 34, 32, 36, 20, 20, 22, 54, 55, 52, 68, e 63 podem ser agrupados como segue:
Ramo...............Folha
2....................0..0..2
3....................2..4..6
4
5....................2..4..5
6....................3..8
Passos para se Construir um Plot de Ramos e Folhas:
1. Definir os ramos e as folhas que você usará. Escolha as unidades para os ramos de modo que o número de folhas a serem mostradas esteja entre 5 e 20.
2. Escreva os ramos numa coluna arranjada com os ramos maenores no topo e os maiores no fundo. Incluir todos os ramos no intervalo de dados, mesmo se existirem alguns ramos com nenhuma folha correspondente.
3. Se as folhas consistem de mais do que um dígito, abandone os dígitos após o primeiro. Você pode arredondar os números para ser mais preciso, mas isto não é necessário para a descrição gráfica a ser útil.
4. Registre a folha para cada medida na linha correspondente no seu ramo. Omitir as decimais, e incluir a chave que define as unidades da folha.
Ver as seguintes figuras:
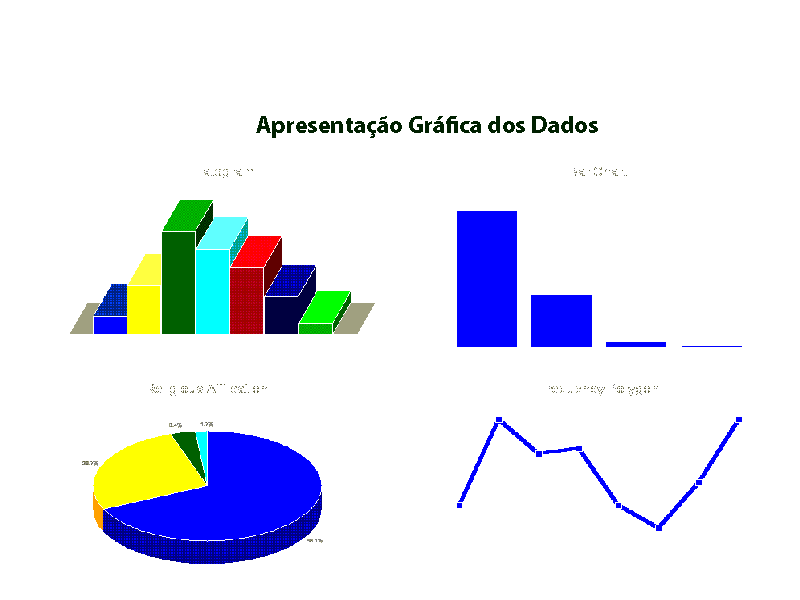
![]()
Links relacionados a esta aula